Cho tứ diện ABCD và ba điểm P,Q,R lần lượt nằm trên cạnh AB, CD, BC; biết PR cắt AC tại I. Xác định giao tuyến của hai mặt phẳng (PQR) và (ACD) là:
A. Qx//AB
B. Qx//BC
C. Qx//AC
D. QI
PB
Những câu hỏi liên quan
Cho tứ diện ABCD và ba điểm P,Q,R lần lượt nằm trên cạnh AB, CD, BC; biết PR//AC. Xác định giao tuyến của hai mặt phẳng (PQR) và (ACD) là:
A. Qx//AB
B. Qx//BC
C. Qx//AC
D. Qx//CD
Đáp án C
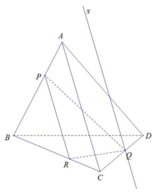
Xét (PQR) và (ACD) có:
Q là điểm chung
AC // PR
⇒ giao tuyến (PQR) và (ACD) là Qx song song với AC
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD và ba điểm P, Q, R lần lượt lấy trên ba cạnh AB, CD, BC. Cho PR // AC và CQ = QD. Gọi giao điểm của AD và (PQR) là S. Chọn khẳng định đúng
A. AD = 3 DS
B. AD = 2 DS
C. AS = 3 DS
D. AS = DS
Đáp án D
Xét (PQR) và (ACD) có:
Q là điểm chung
PR // (ACD) ( do PR // AC)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng d đi qua Q và song song PR
d cắt AD tại điểm S cần tìm
⇒ SQ // AC
Mà Q là trung điểm CD
⇒ S là trung điểm AD
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Các điểm P,Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR=2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Tính tỉ số SA/SD là:
A. 2
B. 1/2
C. 1/3
D. 1
Đáp án A
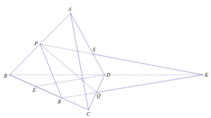
Xét (BCD) có: RQ ∩ BD = K
⇒ K ∈ (ABD)
Xét (ABD) có: PK ∩ AD = S
Gọi E là trung điểm BR
⇒ R là trung điểm đoạn EC
Mà Q là trung điểm CD
⇒ RQ là đường trung bình tam giác DEC
⇒ RQ // DE ⇒ RK // DE
Xét tam giác BRK có: RK // DE và E là trung điểm BR
⇒ D là trung điểm BK
Xét tam giác ABK có: AD là đường trung tuyến cạnh BK
và KP là đường trung tuyến cạnh AB
PK ∩ AD = S
⇒ S là trọng tâm tam giác ABK
⇒ S A S D = 2
Đúng 1
Bình luận (0)
BT
27 tháng 11 2016 lúc 9:05
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .
BT
20 tháng 11 2016 lúc 22:42
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .
BT
18 tháng 11 2016 lúc 18:13
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .
BT
27 tháng 11 2016 lúc 18:58
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .
BT
27 tháng 11 2016 lúc 18:57
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .
BT
19 tháng 11 2016 lúc 10:50
cho tứ diện ABCD và 3 điểm P , Q lần lượt là trung điểm của AB và CD ; điểm R nằm trên cạnh BC sao cho BR=2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD . chứng minh rằng AS=2SD .