Trong không gian với hệ trục tọa độ Oxyz, tính góc giữa hai đường thẳng d 1 : x 1 = y + 1 - 1 = z - 1 2 và d 2 : x + 1 - 1 = y 1 = z - 3 1
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x - 2 1 = y - 1 - 2 = z + 1 3 và mặt phẳng ( α ) : - x + 2 y - 3 z = 0 . Gọi ρ là góc giữa đường thẳng d và mặt phẳng ( α ) . Khi đó, góc ρ bằng
A. 0 °
B. 45 °
C. 90 °
D. 60 °
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là 2 x − 2 y − z = 0 và x + 3 y + z − 1 = 0 . Tính cosin của góc giữa đường thẳng d và trục Oy.
A. 3 35
B. 3 23
C. 3 74
D. 3 6
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x = 2 - t y = 5 z = 1 + t và mặt phẳng ( P ) : y - z + 2 = 0 . Góc giữa đường thẳng d và mặt phẳng (P) là:
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x - y + 2 z + 1 = 0 và đường thẳng d : x - 1 1 = y 2 = z + 1 - 1 . Tính góc giữa đường thẳng d và mặt phẳng (P)
A. 60 °
B. 120 °
C. 150 °
D. 30 °
Chọn D.
Phương pháp: Tính thông qua góc giữa các véc tơ chỉ phương và pháp tuyến của đường thẳng và mặt phẳng đó.

Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là.
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 2 = y - 2 2 = z - 1 3 và đường thẳng d 2 : x = 2 + t y = 1 - 2 t z = t . Gọi φ là góc giữa hai đường thẳng d 1 và d 2 . Tính xấp xỉ .
A. φ ≈ 62 ° 53 '
B. φ ≈ 72 ° 43 '
C. φ ≈ 36 ° 40 '
D. Đáp án khác.
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : x = 1 - t y = 2 + 2 t z = 3 + t và mặt phẳng (P): x-y+3=0. Tính số đo góc giữa đường thẳng d và mặt phẳng (P)
A. 60 °
B. 30 °
C. 120 °
D. 45 °
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : { x = 1 - t y = 2 + 2 t z = 3 + t và mặt phẳng P : x - y + 3 = 0 . Tính số đo góc giữa đường thẳng d và mặt phẳng (P).
A. 60 °
B. 30 °
C. 120 °
D. 45 °
d : { x = 1 - t y = 2 + 2 t z = 3 + t có 1 véc tơ chỉ phương là u → - 1 ; 2 ; 1 và P : x - y + 3 = 0 có véc tơ pháp tuyến là n → 1 , - 1 , 0
Khi đó : góc giữa đường thẳng d và mặt phẳng (P) là:
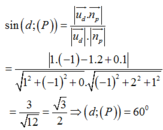
Chọn A.