Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ  thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ  và f(0) = 1. Giá trị của f(1) bằng?

A.  1 e .

B.  1 e .

C.  e .

D. e.

Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ  thỏa mãn f ' x - x f x = 0 ,   f x > 0 ,   ∀ x ∈ ℝ  và f(0) = 1. Giá trị của f(1) bằng?

A.  1 e

B.  1 e

C.  e

D. e

Cho hàm số y = f(x) liên tục trên ℝ, f(x) >0 ∀ x ∈ ℝ  thỏa mãn ln f x + f x - 1 = ln x 2 + 1 e x 2 .Tính  I = ∫ 0 1 x f x d x

A. I =-12

B. I =8

C.I =12

D. I =3/4

Cho f(x) là hàm số chẵn và liên tục trên ℝ  thỏa mãn ∫ - 1 1 f ( x ) d x = 1 . Khi đó giá trị của tích phân ∫ 0 1 f ( x ) d x  là:

A.  1 2

B. 0

C. -1

D. 2

Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f ( 0 ) = 2 3 , f ( x ) > 0 , ∀ x ∈ ℝ và f ( x ) . f ' ( x ) = ( 2 x + 1 ) 1 + f 2 ( x ) , ∀ x ∈ ℝ . Khi đó giá trị f(1) bằng:

Cho hàm số f(x) liên tục trên ℝ +  thỏa mãn f ' x ≥ x + 1 x , ∀ x ∈ ℝ +  và f(1) = 1. Khẳng định nào sau đây là đúng?

A.  f 2 ≥ 5 2 + 2 ln 2

B.  f 2 ≥ 5 2 + ln 2

C.  f 2 ≥ 5

D.  f 2 ≥ 4

Cho f(x) là hàm số liên tục trên R thỏa mãn f x + f ' x = x ,      ∀ x ∈ ℝ   v à   f 0 = 1 . Tính f(1)  

A.  2 e

B.  1 e

C.  e

D.  e 2

Cho hàm số  f(x) có đạo hàm liên tục trên  ℝ  và thỏa mãn f(x) > 0,  ∀ x ∈ ℝ . Biết f(0) = 1 và  f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.

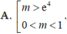
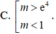
Cho hàm số f(x) liên tục trên ℝ +  thỏa mãn f ' ( x )   ≥ x + 1 x  và f(1) = 1 Khẳng định nào sau đây là đúng?
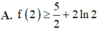
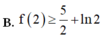