Tính diện tích của hình giới hạn bởi đồ thị hàm số y = ax 3 + bx 2 + cx + d , trục hoành và hai đường thẳng x=1,x=3 (phần được tô như hình vẽ), thì ta được
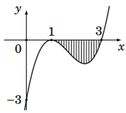
A. S=7/3.
B. S=5/3.
C. S=4/3.
D. S=6/3.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tính diện tích hình phằng giới hạn bởi đồ thị hàm số y = x 4 - 4 x 2 + 1 và đồ thị hàm số y= x 2 - 3
![]()
![]()
![]()
![]()
Phương pháp:
Diện tích hình phẳng giới hạn bởi
đồ thị hàm số y=f(x),y=g(x), các đường thẳng
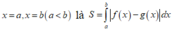
Cách giải:
Xét phương trình hoành độ giao điểm
![]()
![]()
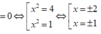
![]()
![]()
![]()
Chọn: A
Tính diện tích hình phằng giới hạn bởi đồ thị hàm số y = x 4 - 4 x 2 + 1 và đồ thị hàm số y = x 2 - 3
A. 8
B. 6
C. 4
D. 2
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị (C) như hình vẽ bên. Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành
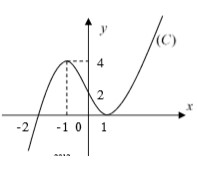
A. 14 3
B. 27 4
C. 31 5
D. 5 31
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.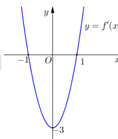 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4
Đáp án D
Dựa vào đồ thị hàm số y = f ' ( x ) ⇒ f ' x = 3 x 2 - 1
Khi đó f x = ∫ f ' x d x = x 3 - 3 x + C .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
f x = 4 f x = 0 ⇒ x 3 - 3 x + C = 4 3 x 2 - 1 = 0 ⇔ x = - 1 C = 2 (Do x < 0 suy ra f x = x 3 - 3 x + 2 C
Cho C ∩ O x ⇒ hoành độ các giao điểm là x = -2,x = 1
Khi đó S = ∫ - 2 1 x 3 - 3 x + 2 d x = 27 4 .
Cho hàm số y = f x = x 4 + 16 x 3 + 21 x 2 - 20 x + 3 và hàm số y = g x = a x + 2 2 có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng S 1 , S 2 , S 3 giới hạn bởi đồ thị hàm số y = f x và đường cong y = g x lần lượt là m, n, p. Tính M = a - b + m - p + n

A. M = 2456 15
B. M = 2531 15
C. M = 2411 15
D. M = 2501 15
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 4 + 4 và y=-x+2
A. 9 2
B. 5 7
C. 8 3
D. 9
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = − x 2 + 4 v à y = - x + 2
A. 9 2
B. 5 7
C. 8 3
D. 9
Đáp án là A
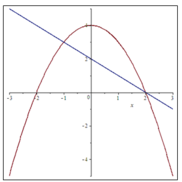
Hoành độ giao điểm của hai hàm số là

Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 2 + 4 và y=-x+2
A. 9/2
B.5/7
C.8/3
D. 9
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x 3 - x và đồ thị hàm số y = x - x 2
A. 9 4
B. 37 12
C. 81 12
D. 13
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x 3 - x = x - x 3 <=> x 3 + x 2 - 2 x = 0
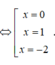
Vậy diện tích của hình phẳng tính là
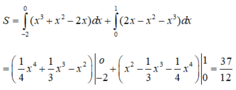
Vậy chọn đáp án B.