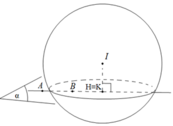
Cho mặt cầu (S) có bán kính bằng 3 (m), đường kính AB. Qua A và B dựng các tia A t 1 , B t 2 tiếp xúc với mặt cầu và vuông góc với nhau. M và N là hai điểm lần lượt di chuyển trên A t 1 , B t 2 sao cho MN cũng tiếp xúc với (S). Biết rằng khối tứ diện ABMN có thể tích V m 3 không đổi. V thuộc khoảng nào sau đây?
A. (17;21)
B. (15;17)
C. (25;28)
D. (23;25)


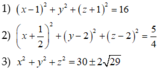
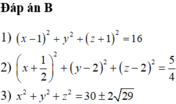
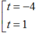








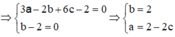
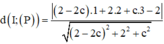
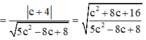
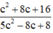 .
.