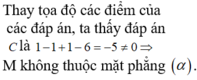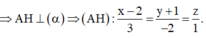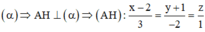Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + + z - 4 = 0 , mặt cầu S : x 2 + y 2 + z 2 - 8 x - 6 y - 6 z + 18 = 0 và điểm M 1 ; 1 ; 2 ∈ α . Đường thẳng d đi qua M và nằm trong mặt phẳng α cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho dây cung AB có độ dài nhỏ nhất. Đường thẳng d có một vectơ chỉ phương là
A. u 1 ⇀ = 2 ; - 1 ; - 1
B. u 1 ⇀ = 1 ; 1 ; - 2
C. u 1 ⇀ = 1 ; - 2 ; 1
D. u 1 ⇀ = 0 ; 1 ; - 1