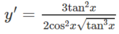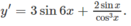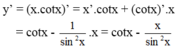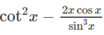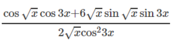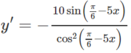Tìm đạo hàm của hàm số sau: y = a + b x + c x 2 4
PB
Những câu hỏi liên quan
Tìm đạo hàm của hàm số sau: y = (x - a)(x - b)
Tìm đạo hàm của hàm số sau: y = tan 3 x
Tìm đạo hàm của hàm số sau: y = sin 2 3 x + 1 cos 2 x
Tìm đạo hàm của các hàm số sau y = x . c o t x
Tìm đạo hàm của hàm số sau: y = x a 2 - x 2
Tìm đạo hàm của các hàm số sau: y = x c o t 2 x
Tìm đạo hàm của các hàm số sau: y = sin x cos 3 x
Tìm đạo hàm của hàm số sau: y = 2 cos π 6 - 5 x
H24
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 20:05
a) Dùng định nghĩa tỉnh đạo hàm của hàm số \(y = x\) tại điểm \(x = {x_0}\).
b) Nhắc lại đạo hàm của các hàm số \(y = {x^2},y = {x^3}\) đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số \(y = {x^n}\) với \(n \in {\mathbb{N}^*}\).
a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
Đúng 0
Bình luận (0)