Tập nghiệm trong C của phương trình z3 + z2 + z + 1 = 0 là:
A.{-1; -i ; i}
B.{-1 ; 1 ; i}
C. -1 ; i
D. 1 ; -1 ; i ; -i
PB
Những câu hỏi liên quan
Tập nghiệm trong C của phương trình z 3 + z 2 + z + 1 = 0 là:
A. {-i; i; 1; -1}
B. {-i; i; 1}
C. {-i; -1}
D. {-i; i; -1}
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) 0 trên tập số phức, tính tổng: A. 2/5 B. 3/5 C. 5/4 D. 6/7
Đọc tiếp
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: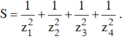 
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
Đúng 0
Bình luận (0)
Phương trình
z
3
-
(
1
+
i
)
z
2
+
(
3
+
i
)
z
-
3
i
0...
Đọc tiếp
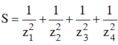
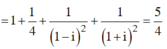
Phương trình z 3 - ( 1 + i ) z 2 + ( 3 + i ) z - 3 i = 0 có tập nghiệm là:
A.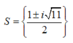 
B.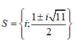 
C.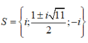 
D.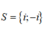 
Gọi
z
1
,
z
2
,
z
3
là các nghiệm của phương trình
i
z
3
-
2
z
2...
Đọc tiếp
Gọi z 1 , z 2 , z 3 là các nghiệm của phương trình i z 3 - 2 z 2 + ( 1 - i ) z + i = 0 .
Biết z 1 là số thuần ảo.
Đặt P = z 2 - z 3 hãy chọn khẳng định đúng?
A. 4<P<5
B. 2<P<3
C. 3<P<4
D. 1<P<2
Gọi
z
1
,
z
2
,
z
3
,
z
4
là bốn nghiệm phức của phương trình
z
4
-
z
2
- 8 0. Trên mặt phẳng tọa độ z gọi A , B , C , D lầ...
Đọc tiếp
Gọi z 1 , z 2 , z 3 , z 4 là bốn nghiệm phức của phương trình z 4 - z 2 - 8 = 0. Trên mặt phẳng tọa độ z gọi A , B , C , D lần lượt là bốn điểm biểu diễn bốn nghiệm z 1 , z 2 , z 3 , z 4 đó. Tính giá trị của P = OA + OB + OC + OD, trong đó O là gốc tọa độ.
A. P = 4
B. P = 2 + 2
C. P = 2 2
D. P = 4 + 2 2
Biết phương trình
a
z
3
+
b
z
2
+
c
z
+
d
0
(
a
,
b
,
c
,
d
∈
R
)
có z1, z2, z3 là các nghiệm, biết rằng
z
3
1
+
2
i
là nghiệm của phương trình. Biết z2 có...
Đọc tiếp
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z 3 = 1 + 2 i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
A. 3
B. 2
C. -2
D. -1
Biết phương trình
a
z
3
+
b
z
2
+
c
z
+
d
0
(
a
,
b
,
c
,
d
∈
R
)
có z1, z2, z3 là các nghiệm, biết rằng z31+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức
w
z...
Đọc tiếp
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z3=1+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
Kí hiệu
z
1
,
z
2
,
z
3
là ba nghiệm của phương trình phức
z
3
+
2
z
2
+
z
-
4
0
. Tính giá trị của biểu thức
T
z
1
+
z...
Đọc tiếp
Kí hiệu z 1 , z 2 , z 3 là ba nghiệm của phương trình phức z 3 + 2 z 2 + z - 4 = 0 . Tính giá trị của biểu thức T = z 1 + z 2 + z 3 .
Gọi
z
1
,
z
2
,
z
3
là ba nghiệm phức của phương trình
z
3
- 1 0. Tính P |
z
1
+
z
2
+
z
3
| A. P 10 B. P 13 C. P 93 D. P 0
Đọc tiếp
Gọi z 1 , z 2 , z 3 là ba nghiệm phức của phương trình z 3 - 1 = 0. Tính P = | z 1 + z 2 + z 3 |
A. P = 10
B. P = 13
C. P = 93
D. P = 0
