Cho số phức z = 3 + i . Điểm biểu diễn số phức 1 z trong mặt phẳng phức là:
A. M 3 10 ; - 1 10
B. M 3 10 ; 1 10
C. M - 3 10 ; - 1 10
D. M - 3 10 ; 1 10
Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A. 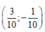
B. ![]()
C. 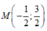
D. 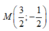
Cho số phức z = 3+ i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A. 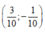
B. 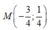
C. 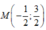
D. 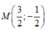
Chọn A.
Ta có : 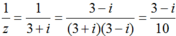
Do đó điểm biểu diễn số phức 1/z trong mặt phẳng phức là: 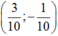
Cho số phức z thỏa mãn 1 + i z + 5 ( 1 − i ) 1 + 2 i = 6 − 6 i . Trong các điểm dưới đây, điểm nào biểu diễn số phức z trong mặt phẳng phức Oxy?
A. M(2;5)
B. N(-2;5)
C. P(2;-5)
D. Q(-2;-5)
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
Trong mặt phẳng phức Oxy, các số phức z thỏa z + 2 i - 1 = z + i . Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3)
![]()
![]()
![]()
![]()
Cho số phức z = - 2 i - 1 . Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2).
B. M(-1;2).
C. M(-2;1).
D. M(2;-1).
Chọn B
Ta có: z = - 2i – 1 = -1 - 2i
Số phức liên hợp của z là ![]() có phần thực là -1, phần ảo là 2.
có phần thực là -1, phần ảo là 2.
Vậy điểm biểu diễn số phức liên hợp là M(-1;2)
Cho số phức z = - 2 i - 1 . Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2).
B. M(2;-1).
C. M(-2;1).
D. M(-1;2).
Chọn D.
Số phức liên hợp của z là z ¯ = - 1 + 2 i có phần thực là -1, phần ảo là 2.
Vậy điểm biểu diễn số phức liên hợp là M(-1;2)
Cho số phức z = ( 1 + i ) 5 . Điểm biểu diễn số phức z nằm trong góc phần tư nào của hệ tọa độ vuông góc của mặt phẳng phức?
A. Góc phân tư thứ IV
B. Góc phân tư thứ I
C. Góc phân tư thứ II
D. Góc phân tư thứ III
Cho số phức z thỏa mãn z - 3 + 4 i = 2 và w = 2z + 1 – i. Trong mặt phẳng phức, tập hợp điểm biểu diễn số phức w là đường tròn tâm I, bán kính R . Khi đó:
A. I (-7;9), R = 16
B. I (-7;9), R = 4
C. I (7;-9), R = 16
D. I (7;-9), R = 4.