Cho hàm số y = 2 x − x 2 . Chọn đẳng thức đúng
A. y 3 . y " + 1 = 0
B. y 3 . y ' − 1 = 0
C. y 2 . y " + 1 = 0
D. y 3 . y " − 1 = 0
Cho hàm số y = 2 x − x 2 . Chọn đẳng thức đúng
A. y 3 . y " + 1 = 0
B. y 3 . y ' − 1 = 0
C. y 2 . y " + 1 = 0
D. y 3 . y " − 1 = 0
Chọn đáp án đúng. Cho hàm số y = 2 x + 1 − x + 2 , khi đó hàm số
A. nghịch biến trên 2 ; + ∞ .
B. đồng biến trên 2 ; + ∞ .
C. nghịch biến trên ℝ \ 2 .
D. đồng biến trên ℝ \ 2 .
Đáp án B
Ta có y ' = 5 2 − x 2 > 0 , ∀ x ∈ D ⇒ Hàm số đồng biến trên các khoảng − ∞ ; 2 và 2 ; + ∞
Cho hàm số y = x + 2 . Chọn khẳng định đúng?
A. Hàm số đạt cực tiểu tại x=0
B. Hàm số đạt cực tiểu tại x=-2
C. Hàm số đạt cực đại tại x=-2
D. Hàm số không có cực trị
Đáp án B
y = x + 2 = x + 2 2
y ' = x + 2 x + 2 2
y ' = 0 ⇔ x = − 2 y ' > 0 ⇔ x ∈ − 2 ; + ∞ ; y ' < 0 ⇔ x ∈ − ∞ ; − 2
Nên hàm số đạt cực tiểu tại x=-2
Cho hàm số y = x + 2 . Chọn khẳng định đúng?
A. Hàm số đạt cực tiểu tại x=0
B. Hàm số đạt cực tiểu tại x=-2
C. Hàm số đạt cực đại tại x=-2
D. Hàm số không có cực trị
Đáp án B
Ta có: y = x + 2 = x + 2 2
Có y ' = x + 2 x + 2 2
y ' = 0 ⇔ x = − 2 y ' > 0 ⇔ x ∈ − 2 ; + ∞ ; y ' < 0 ⇔ x ∈ − ∞ ; − 2
Nên hàm số đạt cực tiểu tại x=-2
Gọi m, n, p lần lượt là số tiềm cận của đồ thị các hàm số
y = 6 - 2 x 3 x + 8 ; y = 4 x 2 + 3 x - 1 3 x 2 + 1 ; y = 11 4 x 2 + x - 2
Bất đẳng thức nào sau đây đúng?
A. m > n > p
B. m > p > n
C. p > m > n
D. n > p > m
Đồ thị hàm số y = 6 - 2 x 3 x + 8 có 2 tiệm cận (đứng, ngang). Suy ra m = 2
Đồ thị hàm số y = 4 x 2 + 3 x - 1 3 x 2 + 1 có 1 tiệm cận (ngang). Suy ra n = 1
Đồ thị hàm số y = 11 4 x 2 + x - 2 có 3 tiệm cận (1ngang, 2 đứng). Suy ra p = 3
Vậy p > m > n
Đáp án C
Cho hàm số y = x + 1 x - 2 . Chọn khẳng định đúng
A. Đồ thị hàm số có đường tiệm cận ngang là x = 2
B. Hàm số nghịch biến trên R
C. Hàm số nghịch biến trên từng khoảng thuộc tập xác định
D. Hàm số có duy nhất một cực trị
Cho hàm số y = x + 1 x - 2 . Chọn khẳng định đúng
A. Đồ thị hàm số có đường tiệm cận ngang là x = 2
B. Hàm số nghịch biến trên R
C. Hàm số nghịch biến trên từng khoảng thuộc tập xác định
D. Hàm số có duy nhất một cực trị
Đáp án C
Tập xác định x ¹ 2
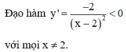
Do đó hàm số nghịch biến trên các khoảng (-¥;2) và (2;+¥)
Cho hàm số y = x + 1 x − 2 . Chọn khẳng định đúng
A. Hàm số có duy nhất một cực trị
B. Hàm số nghịch biến trên từng khoảng thuộc tập xác định
C. Đồ thị hàm số có đường tiện cận ngang là x = 2
D. Hàm số nghịch biến trên R
Cho hàm số y = x - 1 2 x - 2 . Chọn khẳng định đúng.
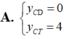
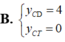
![]()
![]()