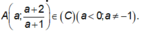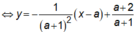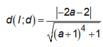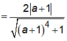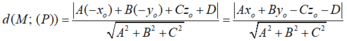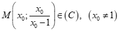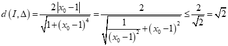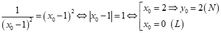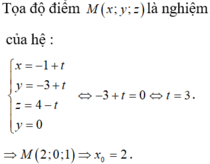Khoảng cách từ điểm M(x0;y0) đường thẳng Δ: ax + by + c = 0 là:
A. d ( M , ∆ ) = a . x 0 + b . y 0 + c a + b
B. d ( M , ∆ ) = a . x 0 + b . y 0 + c a 2 + b 2
C. d ( M , ∆ ) = a . x 0 + b . y 0 a 2 + b 2
D. d ( M , ∆ ) = a . x 0 + b . y 0 + c a 2 + b 2