Cho hình chóp S. ABC có SA vuông góc với đáy, SA = 2BC và B A C ^ = 120 0 . Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Góc giữa hai mặt phẳng (ABC) và (AMN) bằng
A. 45 0
B. 60 0
C. 15 0
D. 30 0
Cho hình chóp S,ABC có SA vuông góc với đáy, S A = 2 B C và B A C ^ = 120 ∘ . Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Góc giữa hai mặt phẳng A B C v à A M N bằng
A. 45 °
B. 60 °
C. 15 °
D. 30 °
Đáp án D
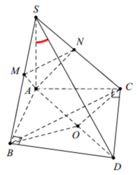
Gọi O là tâm đường tròn ngoại tiếp Δ A B C , D là điểm đối xứng với A qua O.
⇒ O A = O B = O D suy ra tam giác ABD vuồn tại B ⇒ A B ⊥ B D .
Ta có A B ⊥ B D S A ⊥ B D ⇒ B D ⊥ S A B ⇒ B D ⊥ A M suy ra A M ⊥ S B D .
Suy ra A M ⊥ S D . Tương tự, ta chứng minh được A N ⊥ S D
Do đó S D ⊥ A M N . suy ra A B C ; A M N ^ = S A ; S D ^ = A S D ^
Tam giác SAD vuông tại A, có tan A S D ^ = A D S A
Mà đường kính A D = 2 x R Δ A B C = B C sin 120 ∘ = 3 2 x S A
Vậy tan A S D ^ = 3 3 ⇒ A S D ^ = 30 ∘ ⇒ A B C ; A M N ^ = 30 ∘
Cho hình chóp S.ABC có SA vuông góc với đáy, S A = 2 B C v à B A C ^ = 120 ° . Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN)
A. 45 °
B. 60 °
C. 15 °
D. 30 °
Đáp án D
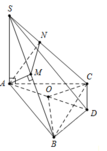
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Và D là điểm đối xứng với A qua O.

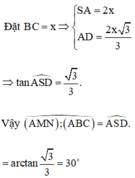
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD = 2 BC , AB = BC = a , SA vuông góc với đáy, SA = a 2 . Tính góc giữa (AC, (SCD)).
A. 60 0
B. 75 0
C. 45 0
D. 30 0
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD=2BC, AB=BC=a. SA vuông góc với đáy, S A = a 2 Tính góc giữa (AC,(SCD))
A. 45 °
B. 75 °
C. 30 °
D. 60 °
Đáp án A
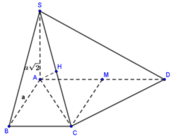
Gọi M là trung điểm AD, khi đó CM = MA = MD nên tam giác ACD vuông tại C.

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD=2BC, AB=BC=a, SA vuông góc với đáy, SA= a 2 . Tính góc giữa (AC, (SCD)).
![]()
![]()
![]()
![]()
Cho hình chóp S. ABCD có đáy là hình thoi cạnh a, Góc ABC =120°, SA vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60. Tính SA Mọi người giúp em với ạ!!!!
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Đáp án B.
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
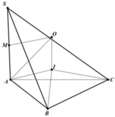
Ta có:
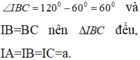
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
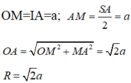
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC
A. a 2 5
B. a 2
C. a 5
D. a 2 4
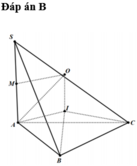
Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có ∠ I B C = 120 ° - 60 ° = 60 ° và IB=BC nên DIBC đều, IA=IB=IC=a
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
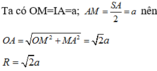
Cho hình chóp S.ABC có SA vuông góc với đáy, SA=2BC và B A C ⏜ = 120 0 . Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).
![]()
![]()
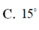
![]()