Để phương trình sin 6x + cos6x = a.| sin2x| có nghiệm, điều kiện thích hợp cho tham số a là:
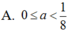
![]()
![]()
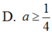
Cho phương trình sin x + m 2 3 + sin 2 x - m 2 3 = 2 sin x - m 2 3 . Gọi S = [a;b] là tập hợp tất cả các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tìm giá trị của P = a 2 + b 2
A. P = 162 49
B. P = 49 162
C. P = 4
D. P = 2
Cho phương trình: sin 6 x + cos 6 x cos 2 x - sin 2 x = 2 m . tan 2 x , trong đó m là tham số. Để phương trình có nghiệm, các giá trị thích hợp của m là
![]()
![]()
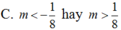
![]()
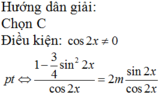
![]()
Đặt t= sin2x ( -1< t< 1). Phương trình trở thành: 3t2 + 8mt – 4 = 0
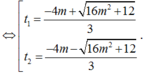
Vì ac< 0 nên phương trình (2) luôn có hai nghiệm trái dấu t2 < 0 < t1.
Do đó (1) có nghiệm 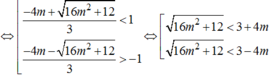
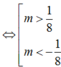
Cho phương trình: 4(sin4x + cos4x ) – 8(sin6x + cos6x) - 4sin24x = m trong đó m là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của m là:
![]()
![]()
![]()
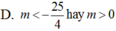

(1) trở thành 4t2 – 2t -6 – m = 0 (2); △ ' = 25 + 4 m .
Để (1) vô nghiệm, ta sẽ tìm m sao cho (1) có nghiệm rồi sau đó phủ định lại.
(1) có nghiệm thì (2) phải có nghiệm thoả t o ∈ - 1 ; 1
Nếu 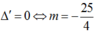 , (2) có nghiệm kép
, (2) có nghiệm kép 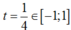 nên
nên ![]() thoả (1) có nghiệm.
thoả (1) có nghiệm.
Nếu ![]() , khi đó (2) phải có hai nghiệm phân biệt thoả
, khi đó (2) phải có hai nghiệm phân biệt thoả 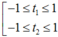
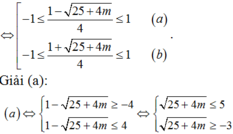
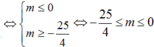
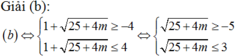
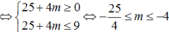

Câu 2 Cho phương trình 2x ^ 2 - 6x + 2m - 5 = 0 ( là tham số) a) Giải phương trình với m = 2 b) Tìm điều kiện của m để phương trình vô nghiệm? có nghiêm kịp? Có 2 nghiêm phân biệt?
a) 2x2 - 6x -1 = 0
delta phẩy = 9 + 2 = 11 = (\(\sqrt{11}\))2
x1 = \(\dfrac{3+\sqrt{11}}{2}\)
x2 = \(\dfrac{3-\sqrt{11}}{2}\)
b) xét delta phẩy có :
9 - 2.(2m-5) = 19 - 4m
+) điều kiện để phương trình vô nghiệm là 19 - 4m < 0 => m > \(\dfrac{19}{4}\)
+) điều kiện để phương trình có nghiệm kép là 19 - 4m = 0 => m = \(\dfrac{19}{4}\)
+) điều kiện để phương trình có 2 nghiệm phân biệt là 19 - 4m > 0
=> m < \(\dfrac{19}{4}\)
Cho hệ phương trình: m 2 x + m + 4 y = 2 m x + y = 1 − y . Để hệ này vô nghiệm điều kiện thích hợp cho tham số m là:
A. m = 0 m = − 2
B. m = 1 m = 2
C. m = − 1 m = 1 2
D. m = − 1 2 m = 3
m 2 x + m + 4 y = 2 m x + y = 1 − y ⇔ m 2 x + m + 4 y = 2 m x + m + 1 y = 1
Ta có: D = m 2 m + 4 m m + 1 = m 3 − 4 m = m m 2 − 4
D x = 2 m + 4 1 m + 1 = 2 m + 1 − m − 4 = m − 2
D y = m 2 2 m 1 = m 2 − 2 m
Nếu D = 0 ⇔ m m 2 - 4 = 0 ⇔ m = 0 m = ± 2
+) Với m = 0 ⇒ D x ≠ 0 nên hệ phương trình vô nghiệm
+) Với m = 2 ⇒ D x = D y = 0 nên hệ phương trình có vô số nghiệm
+) Với m = - 2 ⇒ D x ≠ 0 nên hệ phương trình vô nghiệm
Vậy với m = 0 hoặc m = - 2 thì hệ phương trình vô nghiệm
Đáp án cần chọn là: A
Để phương trình: sin2x + 2(m+1).sinx – 3m( m – 2) = 0 có nghiệm, các giá trị thích hợp của tham số m là:
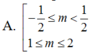
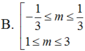
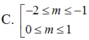
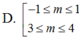
Hướng dẫn giải
Chọn B
Đặt t= sinx. Điều kiện t ∈ - 1 ; 1 . Phương trình trở thành:
t2 + 2(m+1) t – 3m( m- 2)= 0 (1)
Đặt f(t) = t2 + 2(m+ 1) t – 3m( m- 2) .
Phương trình có nghiệm thuộc đoạn [-1; 1] khi và chỉ khi (1) có một nghiệm thuộc [-1; 1] hoặc có hai nghiệm thuộc [-1; 1]
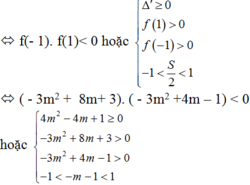
Gọi K là tập hợp tât cả các giá trị của tham số m để phương trình sin 2 x + 2 . sin ( x + π 4 ) - 2 = m có đúng hai nghiệm thuộc khoảng 0 , 3 π 4 . Hỏi là tập con của tập hợp nào dưới đây?
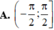
![]()
![]()
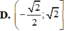
Số giá trị nguyên của tham số m thuộc đoạn - 2018 , 2018 để phương trình m + 1 . sin 2 x - sin 2 x + cos 2 x = 0 có nghiệm là:
A. 4037
B. 4036
C. 2019
D. 2020
Tìm điều kiện của m để phương trình: sin 6 x + 4 cos 6 x = m có nghiệm.
![]()
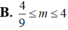
![]()
![]()