Tổng các phân thực của tất cả các số phức z thỏa mãn là số thực và 2 + i z - 5 bằng
A. 2
B. 1
C. -7
D. 6
Gọi S là tập hợp tất cả các giá trị thực của m để tồn tại 4 số phức z thỏa mãn | z + z ¯ | + | z - z ¯ | = 2 và z ( z ¯ + 2 ) - ( z + z ¯ ) - m là số thuần ảo. Tổng các phần tử của S là:
A. c
B. 2 + 1 2
C. 2 - 1 2
D. 1 2
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3
Chọn A.
Gọi số phức cần tìm là z = x = yi.
Ta có:
hay x2 + y2 = 25 (*)
Mặt khác: Số phức có phần thực của nó bằng 2 lần phần ảo nên x = 2y
thay vào phương trình (*) ta được: 5y2 = 25 hay 
Vậy số phức cần tìm là: 
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thoả mãn z. z =1 và |z-3-4i|=m. Tính tổng các phần tử thuộc S.
A. 10.
B. 42.
C. 52.
D. 40.
Gọi S là tập hợp các số phức z thỏa mãn. Tổng giá trị tất cả các phần tử của S bằng
A. 1 - 2 3 i
B. - 3 - 3 3 i
C. 1
D. 1 - 3 i
Đáp án A
Phương pháp: Đặt 
Biến đổi để phương trình trở thành 
Cách giải: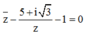 
Đặt 
, ta có:
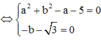
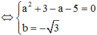
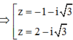=> Tổng giá trị tất cả các phần tử của S bằng
1
-
2
3
i
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Đáp án A
Đặt z=x+yi
Ta có 
suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
(m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N(
3
;1) bán kính r=m
Để tồn tại duy nhất số phức z thì 2 đường tròn phải tiếp xúc với nhau suy ra MN=R+r
Vậy tập S chỉ có 1 giá trị của m
Xác định tất cả các số thực m để phương trình
z 2 - 2 z + 1 - m = 0 có nghiệm phức z thỏa mãn z = 2 .
A. m = 1 ; m = 9 .
B. m = - 3
C. m = - 3 ; m = 1 ; m = 9 .
D. m = - 3 ; m = 9
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z 1 , z 2 thỏa mãn đồng thời các phương trình z - 1 = z - i và z + 2 m = m + 1 . Tổng tất cả các phần tử của S là
A. 1
B. 4
C. 2
D. 3
