Gọi z 1 ; z 2 là hai nghiệm của phương trình z 2 - 4 z + 13 = 0 và A; B lần lượt là hai điểm biểu diễn cho hai số phức z 1 ; z 2 , trong mặt phẳng tọa độ Oxy. Diện tích tam giác OAB bằng
A. 13
B. 12
C. 13 2
D. 6
Gọi S là tập hợp tất cả các số phức z thoả mãn z - 1 = 34 và z + 1 + m i = z + m + 2 i . Gọi z1, z2 là hai số phức thuộc (S) sao cho z 1 - z 2 nhỏ nhất, giá trị của z 1 + z 2 bằng
A.2
B. 2 3
C. 2
D. 3 2
Gọi số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 1 = 1 và ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab=-2
B. ab=2
C. ab=1
D. ab=-1
Đáp án C
Phương pháp
Gọi số phức đã cho có dạng ![]() . Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
. Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
Lời giải chi tiết.
Ta có: ![]()
Do z không là số thực nên ta phải có b ≠ 0 (2)
Ta lại có
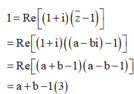
Từ (1), (2), (3) ta có hệ
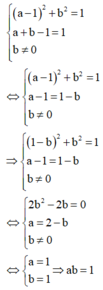
Gọi số phức z= a+bi (a,b∈ R) thỏa mãn |z-1|= 1 và ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab= -2
B. ab= 2
C. ab= 1
D. ab= -1
Gọi số phức z=a+bi (a,b ∈ ℝ ) thỏa mãn z - 1 = 1 v à ( 1 + i ) ( z ¯ - 1 ) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng:
![]()
![]()
![]()
![]()
Gọi số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn |z-1| = 1 và (1+i)( z ¯ -1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. a.b = 1
B. a.b = 2
C. a.b = -2
D. a.b = -1
Đáp án A
Ta có 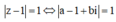
![]()
Số phức ![]()
![]()
có phần số thực bằng a+b-1 = 1(2)
Từ (1), (2) 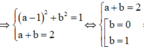
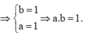
Gọi T là tập hợp số phức z thỏa mãn z − i ≥ 3, z − 1 ≤ 5 . Gọi z 1 , z 2 ∈ T lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2 ?
A. 12 − 2 i
B. − 2 + 12 i
C. 6 − 4 i
D. 12 + 4 i
Đáp án A
Gọi z = a + b i , a , b ∈ ℝ
+ z − 1 ≤ 5 ⇔ a − 1 2 + b 2 ≤ 5 2 C 1
+ z − 1 ≥ 3 ⇔ a 2 + b − 1 2 ≥ 3 2 C 2
C 1 là tập hợp số phức nằm trong hoặc trên đường tròn tâm A 1 ; 0 và bán kính R 1 = 5 .
C 2 là tâp hợp số phức nằm ngoài hoặc trên đường tròn tâm B 0 ; 1 và bán kính R 2 = 3 từ hình vẻ
⇒ z min = z 1 = − 2 i z max = z 2 = 6 ⇒ z 1 + 2 z 2 = 12 − 2 i
Gọi T là tập hợp số phức z thỏa mãn z − i ≥ 3 , z − 1 ≤ 5 . Gọi z 1 , z 2 ∈ T lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2 ?
A. 12 − 2 i
B. - 2 + 12 i
C. 6 − 4 i
D. 12 + 4 i
Gọi số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn |z-1| = 1 và (1+i)( z ¯ -1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a, b bằng
A. a.b = 1
B. a.b = 2
C. a.b = -2
D. a.b = -1
Đáp án A
Ta có ![]()
![]()
Số phức ![]()
![]() có phần số thực bằng
có phần số thực bằng
a + b - 1 = 1(2)
Từ (1), (2) suy ra: 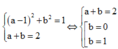
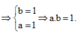
Gọi số phức z = a + bi thỏa mãn z - 1 = 1 và 1 + i z - 1 có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab = -2
B. ab = 2
C. ab = 1
D. ab = -1
Gọi T là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 1 ≤ 5 . Gọi z 1 , z 2 ∈ T lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức z 1 + 2 z 2 .
A. 12 - 2i
B. -2 + 12i
C. 6 - 4i
D. 12 + 4i
Đáp án A
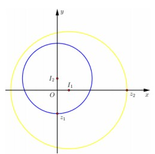
Đặt z = x + y i x , y ∈ ℝ . Khi đó, ta có
z - 1 = x - 1 2 + y 2 ≤ 5 ⇔ x - 1 2 + y 2 ≤ 25 →
Tập hợp các số phức nằm trong hoặc trên đường tròn
tâm I 1 1 ; 0 bán kính R 1 = 5 .
z - i = x 2 + ( y - 1 ) 2 ≥ 3 ⇔ x 2 + ( y - 1 ) 2 ≥ 9 → Tập hợp các số phức nằm ngoài hoặc trên đường tròn tâm , bán kính R 2 = 3 .
Dựa vào hình vẽ, ta thấy rằng z m i n = z 1 = 0 - 2 i = - 2 i z m a x = z 2 = 6 + 0 i = 6 ⇒ z 1 + 2 z 2 = 12 - 2 i .