Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .
A. 130
B. 66
C. 65
D. 131
Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A. m 0 ∈ ( 0 ; 1 / 2 )
B. m 0 ∈ ( 1 / 2 ; 1 )
C. m 0 ∈ ( 3 / 2 ; 2 )
D. m 0 ∈ ( 1 ; 3 / 2 )
Cho số phức z thỏa mãn 1 + i z là số thực và z - 2 = m với m ∈ ℝ
Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán.
Khi đó
A. 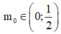
B. 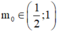
C. 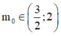
D. 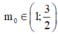
Đáp án D
Phương pháp.Sử dụng giả thiết để tìm được ![]()
Thay vào ![]() và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
m
0
và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
m
0
Lời giải chi tiết.
Giả sử ![]() . Khi đó ta có
. Khi đó ta có
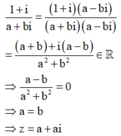
Thay vào ![]() Ta nhận được
Ta nhận được
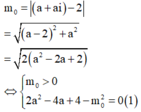
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a.
Khi đó phương trình (1) phải thỏa mãn

Kết hợp với điều kiện ![]() ta suy ra giá trị cần tìm là
ta suy ra giá trị cần tìm là ![]()
Sai lầm.Một bộ phận nhỏ học sinh vẫn có thể quên đưa ra điều kiện ![]() nên hai nghiệm là
nên hai nghiệm là ![]()
Cho số phức z thỏa mãn 1 + i z là số thực và z - 2 = m với m thuộc R Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
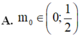
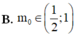
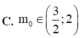
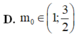
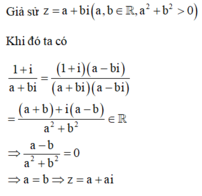
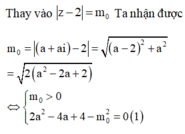
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a. Khi đó phương trình (1) phải thỏa mãn

Đáp án D
trên tập hợp số phức, xét phương trình \(z^2\)-2(2m-1)z+\(m^2\)=0. Có bao nhiêu giá trị của m để phương trình có hai nghiệm phân biệt z1,z2 thỏa mãn \(z1^2\)+\(z2^2\)=2
\(z^2-2\left(2m-1\right)z+m^2=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}z_1+z_2=-\dfrac{b}{a}=2\left(2m-1\right)=4m-2\\z_1z_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
Ta có :
\(z^2_1+z_2^2=2\)
\(\Leftrightarrow\left(z_1+z_2\right)^2-2z_1z_2=2\)
\(\Leftrightarrow\left(4m-2\right)^2-2m^2-2=0\)
\(\Leftrightarrow16m^2-16m+4-2m^2-2=0\)
\(\Leftrightarrow14m^2-16m+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m=\dfrac{1}{7}\end{matrix}\right.\)
Ta có phương trình bậc hai trên tập số phức:
z^2 - 2(2m-1)z + m^2 = 0
Theo định lý giá trị trung bình, nếu z1 và z2 là nghiệm của phương trình trên, thì ta có:
z1 + z2 = 2(2m-1) và z1z2 = m^2
Từ phương trình z1^2 + z2^2 = 2, ta suy ra:
(z1+z2)^2 - 2z1z2 = 4
Thay z1+z2 và z1z2 bằng các giá trị đã biết vào, ta được:
(2(2m-1))^2 - 2m^2 = 4
Đơn giản hóa biểu thức ta có:
m^2 - 4m + 1 = 0
Suy ra:
m = 2 + √3 hoặc m = 2 - √3
Vậy, để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, ta cần phải có m = 2 + √3 hoặc m = 2 - √3.
Kết luận: Có hai giá trị của m để phương trình có hai nghiệm phân biệt thỏa mãn z1^2 + z2^2 = 2, đó là m = 2 + √3 hoặc m = 2 - √3.
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m
![]()
![]()
![]()
![]()
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 8 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m ?
D. 2 ; 2
B. 2 ; 2 2
C. 2 ; 2
D. 2 ; 2 2
Đặt z=x+yi ta có hệ đều kiện:
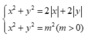
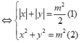
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
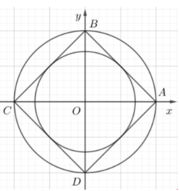
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông 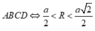
![]()
Chọn đáp án D.
Tìm tập hợp tất cả các giá trị của tham số m để có đúng 4 số phức z thỏa mãn đồng thời các điều kiện z + z ¯ + z - z ¯ = z 2 và z = m ?
A. 2 ; 2 2
B. 2 ; 2 2
C. 2
D. 2 ; 2 2
Cho hai số phức z, ω thỏa mãn z - 1 = z + 3 - 2 i ; ω = z + m + i với m ∈ ℝ là tham số. Giá trị của m để ta luôn có là
A. 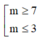
B. 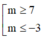
C. 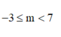
D. 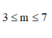
Đáp án B
Ta có:

Tập hợp điểm M biểu diễn w là trung trực của ![]() nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
nên là đường thẳng d qua trung điểm I(m-1;2) và có
n
→
(
4
;
-
2
)
![]()
Đặt ![]()
Do ω ⩾ 2 5 nên M nằm ngoài đường tròn tâm O bán kính R= 2 5
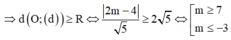
Cho số phức z = 2 + 6 i 3 - i m m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Chọn B.
+ Ta có 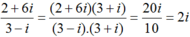
Do đó: 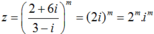
+ để z là số thuần ảo khi và chỉ khi m = 2k + 1
+ Mà 0 ≤ m ≤ 50 nên 0 ≤ 2k + 1 ≤ 50
Suy ra: -1/2 ≤ k ≤ 24,5
Kết hợp với điều kiện k nguyên nên k ∈ {0;1;2;3...24}
Với 25 giá trị của k cho ta tương ứng 25 giá trị m thỏa yêu cầu đề bài.