Số phức z nào dưới đây thỏa mãn (2-i) z 2 + ( 4 + 3 i ) z - 5 ( 1 - i ) = 0 ?
A. z = i
B. z = 1 + i
C. z = 1 - i
D. z = 1
Cho số phức z thỏa mãn ( 1 + i ) z + ( 3 - i ) z ¯ = 2 - 6 i Mệnh đề nào dưới đây đúng?
A. z có phần thực và phần ảo đều âm
B. z có phần thực và phần ảo đều dương
C. z có phần thực dương và phần ảo âm
D. z có phần thực âm và phẩn ảo dương
Cho số phức z thỏa mãn (1+i)z + (3-i) z ¯ = 2 - 6i. Mệnh đề nào dưới đây đúng?
A. z có phần thực và phần ảo đều âm.
B. z có phần thực và phần ảo đều dương.
C. z có phần thực dương và phần ảo âm.
D. z có phần thực âm và phẩn ảo dương.
Xét số phức z thỏa mãn 2|z - 1 | + 3| z - i | ≤ 2 2 . Mệnh đề nào dưới đây đúng?
![]()


Chọn D.
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Số phức z - 1có điểm biểu diễn A(x - 1; y) và z - 1 có điểm biểu diễn là B(x; y - 1).
Ta có
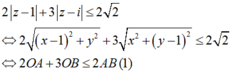
Mà 2OA + 3OB = 2OA + 2OB + OB ≥ 2 AB + OB (2)
Từ (1) và (2) suy ra 2AB + OB ≤ 2AB khi và chỉ khi B và O trùng nhau
Khi đó x; x = 0 và y = 1.
Khi đó z = i ⇒ |z| = 1.
Cho số phức z thỏa mãn 2 z = i ( z ¯ + 3 ) . Điểm nào dưới đây là điểm biểu diễn số phức z?
A. (-1; -2)
B. (2; 1)
C. (-2; -1)
D. (1; 2)
Xét số phức z thỏa mãn ( 1 + 2 i ) z = 10 z - 2 + i . Mệnh đề nào dưới đây đúng?
A. 3 2 < z < 2
B. z > 2
C. z < 1 2
D. 1 2 < z < 3 2
Đáp án D.
Phương pháp: Chuyển vế, lấy mođun hai vế.
Cách giải:
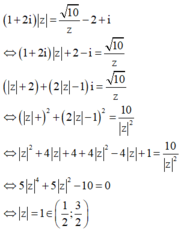
Xét số phức z thỏa mãn ( 1 + 2 i ) z = 10 z - 2 + i . Mệnh đề nào dưới đây đúng?
A. 3 2 < z < 2
B. z > 2
C. z < 1 2
D. 1 2 < z < 3 2
Đáp án D
Phương pháp:
Chuyển vế, lấy mođun hai vế.
Cách giải:
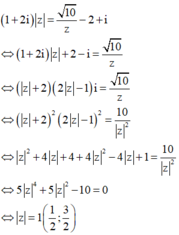
Xét số phức z thỏa mãn ( 1 + 2 i ) z = 10 z - 2 + i . Mệnh đề nào dưới đây đúng?
A. 3 2 < z < 2
B. z > 2
C. z < 1 2
D. 1 2 < z < 3 2
Đáp án D.
Phương pháp: Chuyển vế, lấy mođun hai vế.
Cách giải:
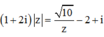
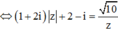
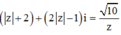
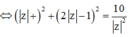
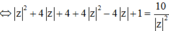
![]()
Cho số phức z thỏa mãn (1+i)z+(3-i) z ¯ =2-6i. Khẳng định nào sau đây đúng
A. z có phần thực và phần ảo đều dương.
B. z có phần thực và phần ảo đều âm
C. z có phần thực dương và phần ảo âm
D. z có phần thực âm và phần ảo dương.
Đường nào dưới đây là tập hợp các các điểm biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện z − i = z + i ?
A. Một đường thẳng
B. Một đường tròn
C. Một đường elip
D. Một đoạn thẳng.
Đáp án A.
Gọi z = x ; y khi đó điều kiện trở thành:
x 2 + y − 1 2 = x 2 + y + 1 2 ⇔ y = − 1
Như vậy quỹ tích là một đường thẳng.