Gọi a,b lần lượt là phần thực và phần ảo của số phức z = | 1 - 3 i | ( 1 + 2 i ) + | 3 - 4 i | ( 2 + 3 i ) . Giá trị của a-b là
A.7
B.-7
C.31
D.-31
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z thỏa mãn 5 z ¯ + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a + b bằng
A. 13
B. -5
C. 9
D. 5
Gọi a và b lần lượt là phần thực và phần ảo của số phức z = 1 + 1 + i + 1 + i 2 + . . . + 1 + i 20 . Tính a +b.
A. 1 - 2 11
B. 1 - 2 20
C. 1.
D. 1 + 2 11
Cho số phức z thỏa mãn ( 2 − 3 i ) z + ( 4 + i ) z ¯ + ( 1 + 3 i ) 2 = 0 . Gọi a, b lần lượt là phần thực và phần ảo của số phức z. Khi đó 2 a - 3 b bằng
A. 1
B. 4
C. 11
D. -19
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z=1-i thì
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Chọn C.
Ta có: ( 1 + i)2(2 - i) z = 8 + i + (1 + 2i)z
Nên z[( 1 + i)2(2 -i) – (1 + 2i) ] = 8 + i
Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i
![]()
Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.
Gọi a, b lần lượt là phần thực và phần ảo của số phức z = 1 - 3 i ( 1 + 2 i ) + 3 - 4 i ( 2 + 3 i ) . Giá trị của a-b là
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính P = a 2 + b 2
A. P = 5
B. P = 7
C. P = 13
D. P = 25
Ta có
2
+
i
z
+
2
1
+
2
i
1
+
i
=
7
+
8
i
![]()
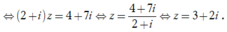
Suy ra 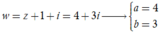
![]()
Chọn D.
Gọi a, b lần lượt là phần thực và phần ảo của số phức z = 1 - 3 i 1 + 2 i + 3 - 4 i 2 + 3 i . Giá trị của a - b là
A. 7
B. -7
C. 31
D. -31