Gọi m là số thực để hàm số y= (x+ m)3 đạt giá trị lớn nhất bằng 8 trên đoạn [1; 2]. Khẳng định nào dưới đây đúng?
A. -2< m< 0
B.2< m< 4
C.-1< m< 2
D. 0 <m< 3
PB
Những câu hỏi liên quan
Gọi M là giá trị lớn nhất của hàm số
y
x
3
-
3
x
2
+
x
+
m
xét trên đoạn [2;4],
m
0
là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng. A.
1...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m 0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. - 7 < m 0 < - 5
C. - 4 < m 0 < 0
D. m 0 < - 8
Gọi M là giá trị lớn nhất của hàm số y
x
3
-
3
x
2
+
x
+
m
xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng. A. 1
m
0
5 B. -7
m...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. -7 < m 0 < -5
C. -4 < m 0 < 0
D. m 0 < -8
Chọn D.
Xét hàm số 
hàm số liên tục trên R
Có 
đồng biến trên [2;4]
Nên 
Do đó 
Ta có 
Dấu bằng xảy ra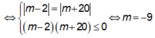 
Vậy 
Đúng 0
Bình luận (0)
câu 19: Tìm giá trị thực của tham số m khác 0 để hàm số y= mx^2-2mx-3m-2 có giá trị nhỏ nhất bằng -10 trên R
câu 20: Gọi S là tập hợp tất cả giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y=f(x)=4x^2-4mx+m^2-2m trên đoạn [-2;0] bằng 3 . Tính tổng T các phần tử của S
Gọi A, a lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y
x
3
-
3
x
+
m
trên đoạn [0;2]. Gọi S là tập các giá trị thực của tham số m để Aa 12. Tổng các phần tử của S bằng A. 0 B. 2 C. -2 D. 1
Đọc tiếp
Gọi A, a lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y = x 3 - 3 x + m trên đoạn [0;2]. Gọi S là tập các giá trị thực của tham số m để Aa = 12. Tổng các phần tử của S bằng
A. 0
B. 2
C. -2
D. 1
Chọn A
Kiến thức bổ sung: Dạng toán tìm GTLN, GTNN của hàm số y = |u(x)| trên đoạn [a;b]
Gọi M, m lần lượt là GTLN, GTNN của hàm số u(x) trên đoạn [a;b]
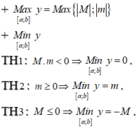
Đặt: 
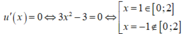
Ta có: 
Suy ra: 
TH1: 
(loại)
(vì ko thỏa mãn giả thiết Aa = 12)
TH2: 
Từ giả thiết: Aa = 12 
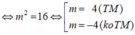
TH3: 
Từ giả thiết: Aa = 12 
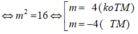
Kết hợp các trường hợp suy ra: S = {-4;4}
Vậy tổng các phần tử của bằng: (-4) + 4 = 0.
Đúng 0
Bình luận (0)
Cho hàm số f(x)(2
x
+m)/(√x+1) với m là tham số thực, m1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là A. 1 B. 3 C. 0 D. 2
Đọc tiếp
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
x
+
m
x
+
1
trên đoạn [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây là đúng? A. 0 m 4 B. 4 m 8 C. 8 m 10 D. m 10
Đọc tiếp
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + m x + 1 trên đoạn [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây là đúng?
A. 0 < m < 4
B. 4 < m < 8
C. 8 < m < 10
D. m > 10
Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.
Đúng 0
Bình luận (0)
Cho hàm số f(x) |3x4 – 4x3 – 12x2 + m|. Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1; 3] Giá trị nhỏ nhất của M bằng C. 16
Đọc tiếp
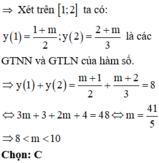
Cho hàm số f(x) = |3x4 – 4x3 – 12x2 + m|. Gọi M là giá trị lớn nhất của hàm số trên đoạn [-1; 3] Giá trị nhỏ nhất của M bằng
C. 16
Gọi S là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = | x 3 - 3 x + m | trên đoạn [0;2] bằng 3. Số phần tử của S là:
A. 0
B. 2
C. 3
D. 1
Chọn B
Xét hàm số g(x) = x 3 - 3 x + m trên ℝ
Bảng biến thiên của hàm số g(x):
Đồ thị của hàm số y = |g(x)| thu được bằng cách giữ nguyên phần đồ thị phía trên trục hoành của (C): y = g(x), còn phần đồ thị phía dưới trục hoành của (C): y = g(x) thì lấy đối xứng qua trục hoành lên trên. Do đó, ta có biện luận sau đây:
Ta xét các trường hợp sau:
Khi đó: 
nên
Như vậy 
(loại)
Khi đó: 
, nên
Như vậy 
(thỏa mãn)
(loại)
do đó
(thỏa mãn)
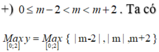
do đó
(thỏa mãn)
Suy ra S = {-1;1}. Vậy chọn B
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
x
-
m
2
x
+
4
với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1 A. m 2 B. m 0 C.
m
6
D. m 3
Đọc tiếp
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
