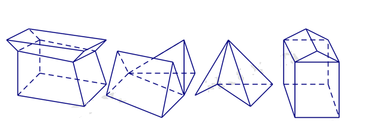
Số hình đa diện lồi trong các hình dưới đây là:
A. 3
B. 0
C. 1
D. 2
PB
Những câu hỏi liên quan
Số hình đa diện lồi trong các hình dưới đây là:
A. Ba mươi
B. Mười sáu
C. Mười hai
D. Hai mươi
Chọn A
Hình mười hai mặt đều có số đỉnh là 20 (SGK HH12).
Đúng 0
Bình luận (0)
Số hình đa diện lồi trong các hình dưới đây là
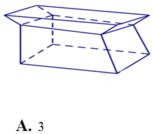
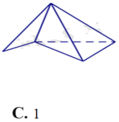
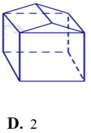
Chọn C
Quan sát bốn hình trên ta thấy chỉ có một hình thứ tư từ trái qua là hình đa diện lồi vì lấy bất kỳ hai điểm nào thì đoạn thẳng nối hai điểm đó nằm trong khối đa diện.
Vậy chỉ có một đa diện lồi.
Đúng 0
Bình luận (0)
Mỗi hình dưới đây gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó).Số đa diện lồi trong các hình vẽ trên là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Mỗi hình dưới đây gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó).
Số đa diện lồi trong các hình vẽ trên là:
A. 1
B. 2
C. 3
D. 4
Đáp án B
Hai đa diện lồi là hình 1 và 4.
Đúng 0
Bình luận (0)
Khẳng định nào sau đây sai?
A. Hình lập phương là đa diện lồi.
B. Tứ diện là đa diện lồi.
C. Hình hộp là đa diện lồi.
D. Hình tạo bởi hai khối lăng trụ có chung nhau một mặt bên là một hình đa diện lồi.
Chọn D.
Hình tạo bởi hai khối lăng trụ lục giác đều bằng nhau có chung nhau một mặt bên không phải là hình đa diện lồi.
Đúng 0
Bình luận (0)
Trong các hình dưới đây hình nào không phải đa diện lồi? A. Hình (III). B. Hình (I). C. Hình (II) . D. Hình (IV).
Đọc tiếp
Trong các hình dưới đây hình nào không phải đa diện lồi?
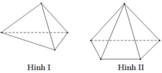
A. Hình (III).
B. Hình (I).
C. Hình (II) .
D. Hình (IV).
Đáp án là D
Khối đa diện (H) được gọi là khối đa diện lồi khi đoạn thẳng nối hai điểm bất kì của (H) đều thuộc (H).
Hình (IV) có đoạn thẳng AB không thuộc khối.
Đúng 0
Bình luận (0)
Trong các hình dưới đây hình nào không phải đa diện lồi? A. Hình (II). B. Hình (I). C. Hình (IV). D. Hình (III).
Đọc tiếp
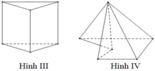
Trong các hình dưới đây hình nào không phải đa diện lồi?
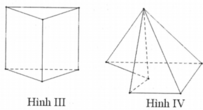
A. Hình (II).
B. Hình (I).
C. Hình (IV).
D. Hình (III).
Đáp án C
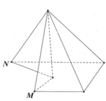
Ta có đường nối hai điểm MN không thuộc hình IV nên đây không phải là đa diện lồi
Đúng 0
Bình luận (0)
Trong các hình dưới đây, hình nào không phải đa diện lồi A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
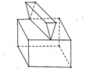
Trong các hình dưới đây, hình nào không phải đa diện lồi
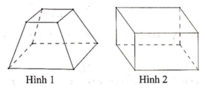
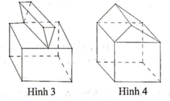
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Chọn C
Áp dụng các tính chất của khối đa thức diện lồi (H)
“Đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H)’’
Đúng 0
Bình luận (0)
Trong các hình dưới đây hình nào không phải đa diện lồi? A. Hình (IV) B. Hình (III) C. Hình (II) D. Hình (I)
Đọc tiếp
Trong các hình dưới đây hình nào không phải đa diện lồi?
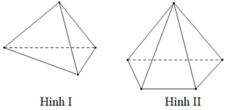
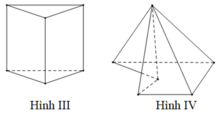
A. Hình (IV)
B. Hình (III)
C. Hình (II)
D. Hình (I)
Chọn A
Ta có đường nối hai điểm MN không thuộc hình IV nên đây không phải là đa diện lồi.
Đúng 0
Bình luận (0)
Trong các hình dưới đây, hình nào không phải đa diện lồi
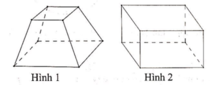
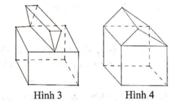
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Chọn đáp án C
Áp dụng các tính chất của khối đa thức diện lồi
“Đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H)"
Đúng 0
Bình luận (0)