Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với AB=a, AC=2a và B A C = 120 ° , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. 4 a 3 5
PB
Những câu hỏi liên quan
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với
A
B
a
,
A
C
2
a
và
B
A
C
^
120
°
,
A
A
2
a
5
. Tính thể tích V của khối lăng trụ đã cho. A.
V...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với A B = a , A C = 2 a và B A C ^ = 120 ° , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. V = 4 a 3 5
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với AB a, AC 2a và BAC
120
0
,
A
A
2
a
5
. Tính thể tích V của khối lăng trụ đã cho. A. V
a
3
15
B. V
4
a
3
5...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với AB = a, AC = 2a và BAC = 120 0 , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. V = 4 a 3 5
Phương pháp:
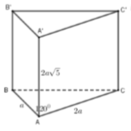
Thể tích lăng trụ V = Bh với B là diện tích đáy, h là chiều cao.
Diện tích tam giác ABC là:
Thể tích lăng trụ
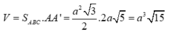
Chọn A.
Đúng 0
Bình luận (0)
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với ABACa,
∠
B
A
C
120
°
, mặt phẳng (A’BC’) tạo với đáy một góc
60
°
. Tính thể tích của khối lăng trụ đã cho bằng: A.
3
3...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB=AC=a, ∠ B A C = 120 ° , mặt phẳng (A’BC’) tạo với đáy một góc 60 ° . Tính thể tích của khối lăng trụ đã cho bằng:
A. 3 3 a 3 8
B. 9 a 3 8
C. a 3 3 8
D. 3 a 3 8
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân ABC với
A
B
A
C
a
;
B
A
C
^
120
∘
Mặt phẳng (AB’C’) tạo với đáy góc 30 độ Tính thể tích V của khối lăng trụ đã cho. A.
V
a
3
6...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân ABC với A B = A C = a ; B A C ^ = 120 ∘ Mặt phẳng (AB’C’) tạo với đáy góc 30 độ Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 6
B. V = a 3 8
C. V = 3 a 3 8
D. V = 9 a 3 8
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, Biết AC a
2
và AB a
37
. Tính thể tích V của khối lăng trụ ABC.A’B’C’ A. V 6
a
3
B. V
a
3
C. V 3
a
3
D. V 9
a
3
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, Biết AC = a 2 và AB = a 37 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 6 a 3
B. V = a 3
C. V = 3 a 3
D. V = 9 a 3
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB2a, BCa. Biết thể tích khối lăng trụ ABC.A’B’C’ bằng
a
3
, chiều cao của hình lăng trụ đã cho bằng A. a/2. B. a. C. 3a. D. 3a/2.
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=2a, BC=a. Biết thể tích khối lăng trụ ABC.A’B’C’ bằng a 3 , chiều cao của hình lăng trụ đã cho bằng
A. a/2.
B. a.
C. 3a.
D. 3a/2.
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuống cân tại A, Biết
A
C
a
2
và
A
B
a
37
Tính thể tích V của khối lăng trụ ABC.A’B’C’ A.
V
6
a
3
B.
V
a
3
C.
V
3
a
3...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuống cân tại A, Biết A C = a 2 và A B = a 37 Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 6 a 3
B. V = a 3
C. V = 3 a 3
D. V = 9 a 3
Đáp án A
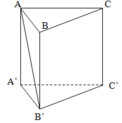
A C = a 2 ⇒ A B = B C = a ⇒ B B ' = 37 a 2 − a 2 = 6 a V = 6 a . 1 2 . a . a = 3 a 3
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABC.ABC có đáy là tam giác cận tại A,ABAC2a,
C
A
B
^
120
°
góc giữa (ABC) và (ABC) là
45
°
Thể tích lăng trụ là A.
V
2
a
3
3
B.
V
a
3
3
C.
V...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cận tại A,AB=AC=2a, C A B ^ = 120 ° góc giữa (A'BC) và (ABC) là 45 ° Thể tích lăng trụ là
A. V = 2 a 3 3
B. V = a 3 3
C. V = a 3 3 3
D. V = a 3 3 2
Đáp án B
Kẻ A P ⊥ B C ( P ∈ B C ) ⇒ A ' P A ^ = 45 ° ⇒ A A ' = A P
Mà cos 60 ° = A P A B = 1 2 ⇒ A P = a ⇒ A A ' = a
⇒ V = A ' A . S A B C = a . 1 a . sin 120 ° = a 3 3
Đúng 0
Bình luận (0)
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB a, AA 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A
.
a
3
11
4
B
.
a
3
11...
Đọc tiếp
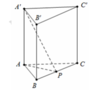
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB = a, AA'= 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A . a 3 11 4
B . a 3 11 12
C . a 3 47 8
D . 3 a 3 4
Đáp án A
Xét ∆AOA’, ta có:
AO2 + OA’2 = AA’2
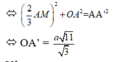
Vậy 
Đúng 0
Bình luận (0)