Số điểm cực trị của hàm số y = x − 1 2017 là
A. 0
B. 2017
C. 1
D. 2016
Cho hàm số y = f(x) = ax4 + bx2 + c biết a > 0, c > 2017 và a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 3
C. 7
D. 5
Cho hàm số f ( x ) = a x 4 + b x 2 + c v ớ i a > 0 , c > 2017 , a + b + c < 2017 . Số cực trị của hàm số y = | f ( x ) - 2017 | là
A. 1
B. 5
C. 3
D. 7
Đáp án D
Phương pháp:
+) Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017
+) Tìm số điểm cực trị của hàm số h(x) bằng cách giải phương trình h'(x) = 0
+) Xác định dấu của h(0); h(1); h(-1) và vẽ đồ thị hàm số y = h(x), từ đó vẽ đồ thị hàm số y = |h(x)| và kết luận.
Cách giải:
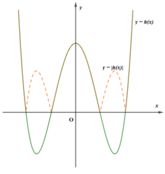
Xét hàm số h(x) = f(x) - 2017 = ax4 + bx2 + c - 2017,
với a > 0, c > 2017, a + b + c < 2017 nên b < 0
![]()
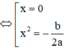
![]()
Ta có: h(0) = c - 2017 > 0, h(-1) = h(1) = a + b + c - 2017 < 0
⇒ h(0).(h-1) < 0, h(0).h(1) < 0
⇒ ∃ x1, x2: x1 ∈ (-1;0), x2 ∈ (0;1) mà h(x1) = h(x2) = 0
Do đó, đồ thị hàm số y = h(x) và y = |h(x)| dạng như hình vẽ bên.
Vậy, số cực trị của hàm số y = |f(x) - 2017| là 7
Cho hàm số f ( x ) = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x - 2017 là
A. 1
B. 5
C. 3
D. 7
Đáp án D.
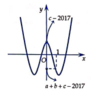
Xét hàm số g ( x ) = f ( x ) - 2017 = a x 4 + b x 2 + c - 2017 là hàm trùng phương nên đồ thị hàm số nhận trục Oy làm trục đối xứng và luôn nhận x = 0 là một điểm cực trị.
Ta có g ( 0 ) = c - 2017 > 0 ( d o x > 2017 ) g ( 1 ) = a + b + c - 2107 < 0 ( d o a + b + c < 2017 ) ⇒ g ( 0 ) . g ( 1 ) < 0 ⇒ phương trình g ( x ) = 0 có nghiệm ( 0 ; 1 ) .
Lại có lim x → + ∞ g ( x ) = lim x → + ∞ = x 4 a + b x 2 + c - 2017 x 4 = + ∞ ( d o a > 0 ) nên tồn tại x = x 0 đủ lớn ( x 0 → + ∞ ) sao cho g ( x 0 ) > 0 ⇒ g ( 1 ) . g ( x 0 < 0 ⇒ ) phương trình g ( x ) = 0 có nghiệm trên 1 ; + ∞ .
Như vậy, với x > 0 thì phương trình g (x) =0 có ít nhất hai nghiệm nên đồ thị hàm số g (x) cắt Ox tại ít nhất hai điểm nằm bên phải trục tung. Suy ra phương trình g (x) có đúng 4 nghiệm hay đồ thị hàm số g(x) cắt Ox tại đúng 4 điểm và có đồ thị như hình bên. Suy ra hàm số y = g(x) có 3 điểm cực trị (1 cực đại, 2 cực tiểu).
Khi đó hàm số y = g ( x ) có 3 + 4 = 7 điểm cực trị.
Cho hàm số f x = a x 4 + b x 2 + c với a > 0, c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x − 2017 là:
A. 1
B. 5
C. 3
D. 7
Đáp án D

Dựa vào 2 dạng của đồ thị hàm số bậc 4 trùng phương khi a > 0
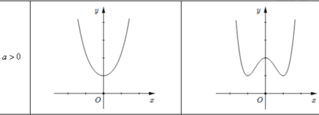
Suy ra hàm số y = f(x) có 3 điểm cực trị và PT: f(x) - 2017 có 4 nghiệm phân biệt
Như vậy PT y ' = 2 f x − 2017 . f ' x 2 f x − 2017 2 = 0 có 7 nghiệm phân biệt do đó hàm số có 7 cực trị.
Cho hàm số f x = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x − 2017 là
A. 1
B. 5
C. 3
D. 7
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Đáp án B
Ta có y , = 0 ⇔ x = 1 x = - 2 x = 3 , y , đổi dấu qua x=1 và x=-2 , y , không đổi dấu qua x=3 nên hàm số có hai cực trị tại x=1 và x=-2
Cho hàm số y = x 2 3 + 2017 , có các khẳng định sau.
I. Hàm số luôn đồng biến trên − ∞ ; + ∞
II. Hàm số có một điểm cực tiểu là x = 0
III. Giá trị lớn nhất bằng 2017.
IV. Hàm số luôn nghịch biến trên − ∞ ; + ∞
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Đáp án B.
Ta có: Tập xác định của hàm số y = x 2 3 + 2017 là R nên y ' = 2 3 x 3
Ta có bảng biến thiên
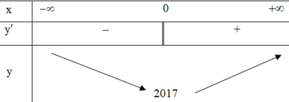
(I) sai vì hàm số chỉ đồng biến trên 0 ; + ∞ ;
(II) đúng là hàm số đạt cực tiểu x = 0; EM NHÌN KĨ BẢNG BIẾN THIÊN NHÉ!
(III) sai vì giá trị nhỏ nhất của hàm số là 2017
(IV) sai vì hàm số nghịch biến trên − ∞ ; 0
Lỗi sai
Ø Có bạn sẽ nhìn nhanh và nhầm y ' = 2 3 x 3 > 0 và kết luận là I đúng
Ø Có bạn sẽ không xét tại x = 0 vì tại đó y' không xác định. Hàm số vẫn đạt cực tiểu tại x = 0. Ta xét các điểm cực trị làm y' = 0 hoặc y' không xác định.
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y=f’(x) như hình bên. Số điểm cực trị của hàm số y=f(x-2017)-2018x+2019 là:
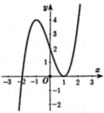
A. 3
B. 1
C. 4
D. 2
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm số y = f ' x như hình vẽ. Số điểm cực trị của hàm số y = f ( x - 2017 ) - 2018 x + 2019 là
A. 1
B. 3
C. 2
D. 0
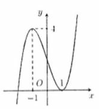
Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới
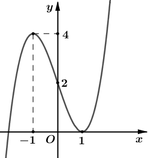
Số điểm cực trị của hàm số y= g( x)= f( x- 2017) – 2018x+ 2019 là
A. 1
B. 2
C.3
D. 4
![]()
Dựa vào đồ thị hàm số y= f’(x) suy ra phương trình f’( x- 2017) = 2018 có 1 nghiệm đơn duy nhất.
Suy ra hàm số y= g( x) có 1 điểm cực trị