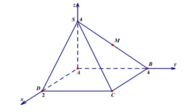
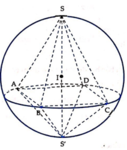
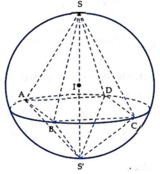
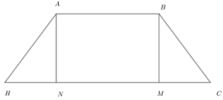
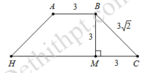
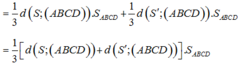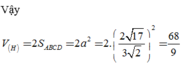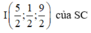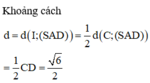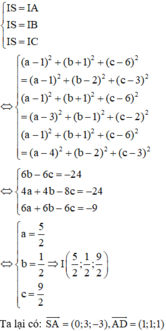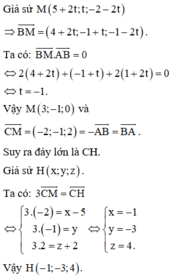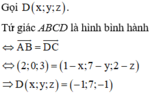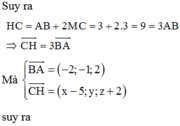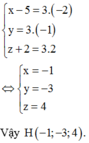Trong không gian với hệ tọa độ Oxyz, cho hình chóp tứ giác đều S.ABCD biết:
A 1 ; 0 ; 0 , B 5 ; 0 ; 0 , C 5 ; 4 ; 0 và chiều cao hình chóp bằng 6. Gọi I(a,b,c) là điểm cách đều 5 đỉnh của hình chóp (với c > 0). Tính giá trị của T = a + 2 b + 3 c .
A. 41
B. 14
C. 23
D. 32