Cho số thực m và hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f 2 x + 2 - x có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?
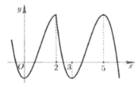
A. 2
B. 3
C. 4
D. 5
Cho hàm số y=f(x) liên tục trên ℝ ,f(2)=3 và có đồ thị như hình vẽ bên
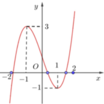
Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình có 4 nghiệm thực phân biệt. f ( x + m ) = 3
A. 2
B. 18
C. 4
D. 19
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=f(x) bằng
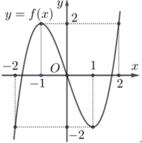
A. 7
B. 3
C. 6
D. 9
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x)) =0 bằng

A. 7
B. 3
C. 5
D. 9
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(f(x))=0 bằng
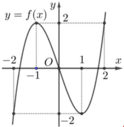
A. 7
B. 3
C. 5
D. 9

Vậy phương trình đã cho có tất cả 9 nghiệm.
Chọn đáp án D.
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Xác định tất cả các giá trị thực của tham số m để phương trình |f(x)| = m có 6 nghiệm thực phân biệt.

A. 0 < m < 4
B. -1 < m < -2
C. 1 < m < 2
D. -1 < m < 2
Đáp án C.
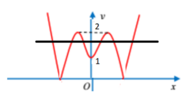
- Lấy đối xứng phần đồ thị hàm số y = f(x) nằm phía dưới trục hoành lên phía trên trục hoành ta được đồ thị hàm số y = |f(x)| (như hình bên). - Số nghiệm của phương trình |f(x)| = m là số giao điểm của đồ thị hàm số y = |f(x)| với đường thẳng y = m. Phương trình |f(x)| = m có 6 nghiệm thực phân biệt ⇔ 1 < m < 2.
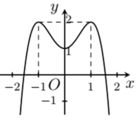
Cho hàm số y =f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + 1 = m có bốn nghiệm thực phân biệt?
![]()
![]()
![]()
![]()
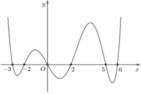
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị của hàm số y = f′(x) như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(x) = f(0) trên đoạn [−3;6] là
A. 4
B. 3.
C. 5.
D. 2.
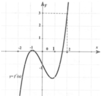
Cho hàm số y=f(x) có đạo hàm liên tục trên R, đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
Cho bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
(
2
x
)
-
1
3
2
3
x
+
2
x
+
2
3
+
m
≥
0
đúng với mọi
x
∈
-
2
;
2
![]()
![]()
![]()
![]()
![]()