Có bao nhiêu giá trị của tham số m để đồ thị hàm số y = mx + x 2 - 2 x + 3 2 x - 1 có một tiệm cận ngang là y = 2.
A. 1.
B. 2.
C. 0.
D. vô số.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 2 - 3 x + 2 x 2 - m x - m + 5 không có đường tiệm cận đứng?
A. 8
B. 10
C. 11
D. 9
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 2 - 3 x + 2 x 2 - m x - m + 5 không có đường tiệm cận đứng?
A. 8
B. 10
C. 11
D. 9
Đáp án là B
Nhận xét:
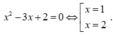
Đặt ![]()
Hàm số đã cho không có đường tiệm cận đứng khi và chỉ khi
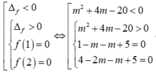
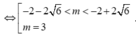
Vì m là số nguyên nên ![]()
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 - 1 - m x + 2 m có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
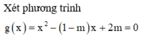
Đồ thị hàm số đã cho có 2 đường tiệm cận đứng ⇔ phương trình g(x) có 2 nghiệm phân biệt
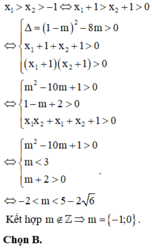
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = 1 + x + 1 x 2 - 1 - m x + 2 m có hai tiệm cận đứng?
A. 0
B. 2
C. 3
D. 1
Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .
Hỏi có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 2 - 3 x + 2 x 2 - m x - m + 5 không có đường tiệm cận đứng?
A. 9
B. 10
C. 11
D. 8
Đáp án B
TH1: Hàm số bị suy biến ⇔ m = 3 ⇒ y = 1 . Khi đó đồ thị hàm số không có TCĐ.
TH2: PT: x 2 - m x - m + 5 = 0 vô nghiệm
⇔ ∆ = m 2 + 4 m - 20 < 0 ⇔ - 2 - 2 6 < m < - 2 + 2 6
Do đó với m ∈ ℤ ⇒ m = - 6 ; - 5 ; - 4 ; - 3 ; - 2 ; - 1 ; 0 ; 1 ; 2 (có 9 giá trị của m).
Vậy có 10 giá trị nguyên của m.
Có tất cả bao nhiêu giá trị khác nhau của tham số m để đồ thị hàm số y = x - 1 x 2 + m x + 4 có 2 đường tiệm cận?
A. 1
B. 2
C. 3
D. 0
Chọn C
Ta có:
![]()
nên đồ thị hàm số luôn có 1 TCN là y = 0
Đồ thị hàm số có 2 đường tiệm cận thì nó chỉ có duy nhất 1 đường tiệm cận đứng
⇔ phương trình x 2 + m x + 4 = 0 có nghiệm x = 1
hoặc phương trình x 2 + m x + 4 = 0 có nghiệm kép (có thể bằng 1)

Vậy có 3 giá trị của m thỏa mãn bài toán
Có tất cả bao nhiêu giá trị khác nhau của tham số m để đồ thị hàm số y = x - 1 x 2 + m x + 4 có hai đường tiệm cận
A. 1
B. 0
C. 2
D. 3
Có bao nhiêu giá trị nguyên thuộc đoạn - 9 ; 9 của tham số m để đồ thị hàm số y = x + 2 x 3 + 3 m x 2 + 2 m 2 + m x + m 2 có đúng bốn đường tiệm cận?
A. 15
B. 14
C. 16
D. 17
Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số C : y = m x − x 2 − 2 x + 2 có tiệm cận ngang?
A. 2
B. 3
C. 1
D. 4.
Đáp án A
Đường thẳng y = y 0 được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f x nếu lim x → + ∞ f x = y 0 hoặc lim x → − ∞ f x = y 0
y = m x − x 2 − 2 x + 2 = m 2 x 2 − x 2 + 2 x − 2 m x + x 2 − 2 x + 2 = m 2 − 1 x 2 + 2 x − 2 m x + x 2 − 2 x + 2
Để hàm phân thức có tiệm cận ngang thì bậc tử phải nhỏ hơn hoặc bằng bậc mẫu ⇔ m 2 − 1 = 0 ⇔ m = 1 m = − 1
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.