Tìm tất cả các giá trị thực của tham số m để hàm số y = sinx − m sinx + m đồng biến trong khoảng 0 ; π 2 .
A. m ≥ 0
B. m > 0
C. − ∞ ; − 1 ∪ 0 ; + ∞
D. − ∞ ; − 1 ∪ 0 ; + ∞
Cho hàm số y = sin x - 3 cos x - m x . Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R
A. m ≤ - 2
B. m ≤ - 3
C. m ≥ 2
D. m ≥ 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin x + m sin x - 1 nghịch biến trong khoảng
A. m > - 1
B. m < - 1
C. m ≤ - 1
D. m ≥ - 1
Cho hàm số y=sinx- 3 cosx-mx Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R.
A.![]()
B.m>2
C.![]()
D.![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin x + m sin x - 1 nghịch biến trong khoảng ( π 2 ; π )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx+ cosx+ mx đồng biến trên ℝ
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx + cosx + mx đồng biến trên ℝ
A. - 2 ≤ m ≤ 2
B. m ≤ - 2
C. - 2 < m < 2
D. m ≥ 2
Đáp án D
YCBT: y ' = cos x - sin x + m ≥ 0 với mọi x ∈ ℝ ⇔ m ≥ sin x - cos x = f x với x ∈ ℝ .
Mà ta có: f x = sin x - cos x = 2 x - π 4 ⇒ - 2 ≤ f x ≤ 2 ⇒ m ≥ 2
Tìm tất cả các giá trị thực của tham số mđể hàm số y = sin x + m sin x - m đồng biến trên ( - π 2 ; 0 ) .
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn C
![]()
![]()
![]() .
.
Hàm số đồng biến trên ![]() khi và chỉ khi
khi và chỉ khi 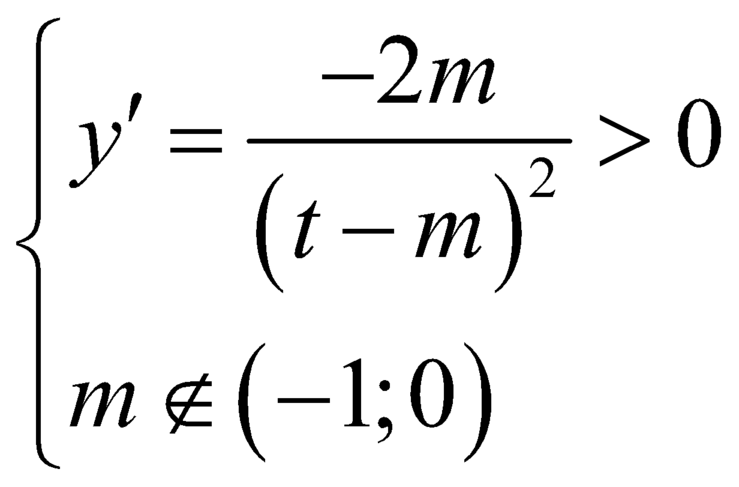
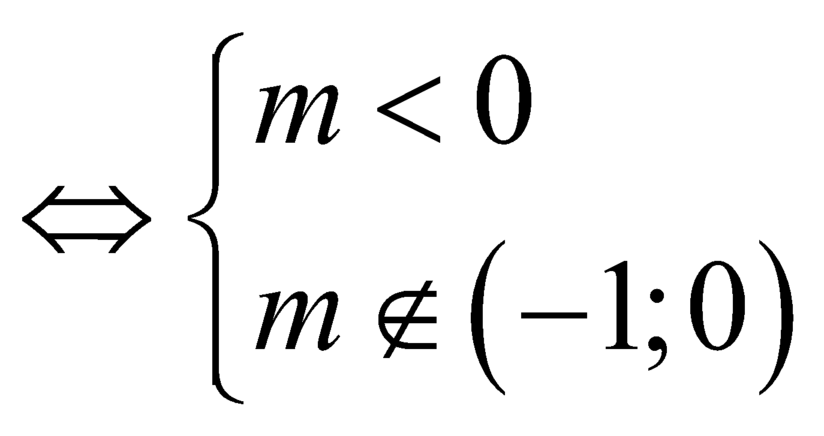
![]()
Cho hàm số y = ( m - 1 ) sin x - 2 sin x - m . Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng ( 0 ; π 2 ) .
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn A
Điều kiện: ![]() . Điều kiện cần để hàm số
. Điều kiện cần để hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là![]() .
.
Ta có : 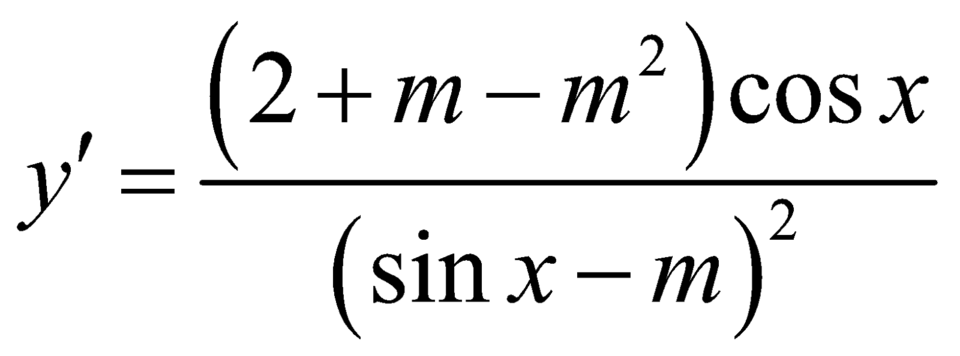 .
.
Ta thấy ![]()
![]() .
.
Để ham số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là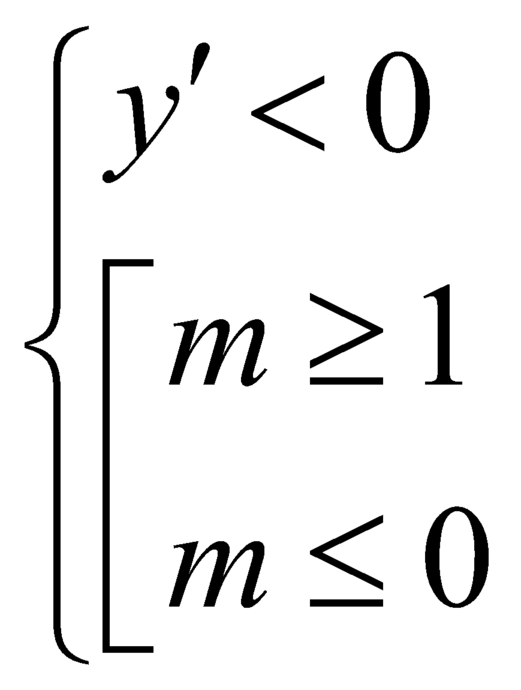
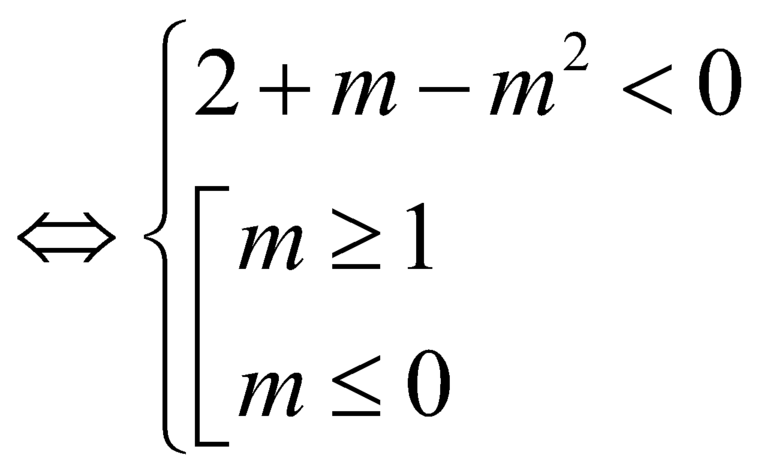
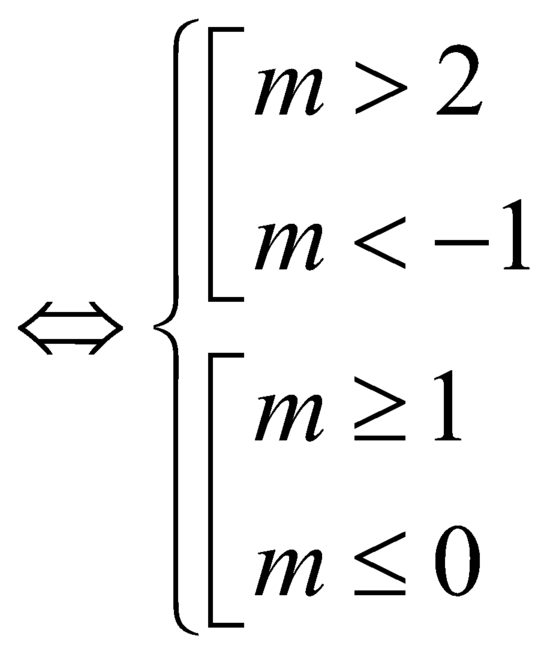
![]() .
.