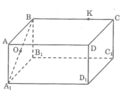
A B C D . A 1 B 1 C 1 D 1 là một hình hộp chữ nhật. Nếu 0 là trung điểm của đoạn AB thì 0 có là trung điểm của đoạn A B 1 hay không?
cho a+b+c+d =2000 và 1/a+b+c+1/b+c+d+1/c+d+a +1/d+a+b=1/40
tính giá trị S= a/b+c+d+b/c+d+a +c/d+a+b+d/a+b+c
Em có cách khác!
\(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
\(\Rightarrow\frac{a+b+c+d}{a+b+c}+\frac{a+b+c+d}{b+c+d}+\frac{a+b+c+d}{c+d+a}\)
\(+\frac{a+b+c+d}{d+a+b}=50\)
\(\Rightarrow\frac{d}{a+b+c}+1+\frac{a}{b+c+d}+1+\frac{b}{c+d+a}+1\)
\(+\frac{c}{d+a+b}+1=50\)
\(\Rightarrow\frac{d}{a+b+c}+\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}=46\)
Đề: \(a+b+c+d=2000\)
\(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
Tính:
\(S=\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}\)
Giải:
Có: \(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
=> \(\frac{1}{2000-d}+\frac{1}{2000-a}+\frac{1}{2000-b}+\frac{1}{2000-c}=\frac{1}{40}\)
<=> \(\frac{2000}{2000-d}+\frac{2000}{2000-a}+\frac{2000}{2000-b}+\frac{2000}{2000-c}=\frac{2000}{40}\)
<=> \(1+\frac{d}{2000-d}+1+\frac{a}{2000-a}+1+\frac{b}{2000-b}+1+\frac{c}{2000-c}=50\)
<=> \(\frac{d}{a+b+c}+\frac{a}{b+c+d}+\frac{b}{a+c+d}+\frac{c}{a+b+d}=46\)
=> \(S=46\)
cho a+b+c+d=4000 và 1/a+b+c + 1/b+c+d+a +1/c+d+a + 1/d+a+b=1/40 .Tính gt của S=a/b+c+d +b/c+d+a +c/d+a+b +d/a+b+c
Ta có S = \(\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}\)
=> S + 4 = \(\left(\frac{a}{b+c+d}+1\right)+\left(\frac{b}{c+d+a}+1\right)+\left(\frac{c}{d+a+b}+1\right)+\left(\frac{d}{a+b+c}+1\right)\)
= \(\frac{a+b+c+d}{b+c+d}+\frac{a+b+c+d}{c+d+a}+\frac{a+b+c+d}{d+a+b}+\frac{a+b+c+d}{a+b+c}\)
\(=\left(a+b+c+d\right)\left(\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}+\frac{1}{a+b+c}\right)\)
\(=4000.\frac{1}{40}=100\)
=> S = 100 - 4 = 96
Cho a+b+c+d=2000 và \(\dfrac{1}{a+b+c}+\dfrac{1}{b+c+d}+\dfrac{1}{c+d+a}+\dfrac{1}{d+a+b}=\dfrac{1}{40}\)
Tính S=\(\dfrac{a}{b+c+d}+\dfrac{b}{c+d+a}+\dfrac{c}{d+a+b}+\dfrac{d}{a+b+c}\)
cho a,b,c,d thỏa mãn a+b+c-5d/d=b+c+d-5a/a=c+d+a-5b/b=d+a+b-5c/c. tính giá trị của P=(1+b+c/a)(1+c+d/b)(1+d+a/c)(1+a+b/d)
Cho \(\dfrac{a+b+c-d}{d}\)=\(\dfrac{b+c+d-a}{a}\)=\(\dfrac{c+d+a-b}{b}\)=\(\dfrac{d+a+b-c}{c}\), (a+b+c+d) khác 0
tính giá trị của biểu thức: P=(1+\(\dfrac{b+c}{a}\))(1+\(\dfrac{c+d}{b}\))(1+\(\dfrac{d+a}{c}\))(1+\(\dfrac{a+b}{d}\))
Lời giải:
Áp dụng TCDTSBN:
$\frac{a+b+c-d}{d}=\frac{b+c+d-a}{a}=\frac{c+d+a-b}{b}=\frac{d+a+b-c}{c}$
$=\frac{a+b+c-d+b+c+d-a+c+d+a-b+d+a+b-c}{d+a+b+c}$
$=\frac{2(a+b+c+d)}{a+b+c+d}=2$
$\Rightarrow a+b+c-d=2d; b+c+d-a=2a; c+d+a-b=2b; d+a+b-c=2c$
$\Rightarrow a+b+c=3d; b+c+d=3a; c+d+a=3b; d+a+b=3c$
Khi đó:
\(P=\frac{a+b+c}{a}.\frac{b+c+d}{b}.\frac{c+d+a}{c}.\frac{a+b+d}{d}\\ =\frac{3d}{a}.\frac{3a}{b}.\frac{3b}{c}.\frac{3c}{d}=81\)
a+b+c-2d/a=b+d+a-2c/b=b+d+c-2a/c=a+c+d-2b/d tính M=(1+a/b)(1+b/c)(1+c/d)(1+d/a)
\(\frac{a+b+c-2d}{a}=\frac{b+d+a-2c}{b}=\frac{b+d+c-2a}{c}=\frac{a+c+d-2b}{d}\)
\(=\frac{\left(a+b+c-2d\right)+\left(b+d+a-2c\right)+\left(b+d+c-2a\right)+\left(a+c+d-2b\right)}{a+b+c+d}\)
\(=\frac{a+b+c+d}{a+b+c+d}=1\)
\(\Leftrightarrow a=b=c=d\).
\(M=\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{d}\right)\left(1+\frac{d}{a}\right)=2^4=16\)
với a,b,c>0
a)1/ab+1/bc+1/ac >= 4/3(1/a+b + 1/b+c + 1/c+a)^2
b)1/(a^2+b^2) + 1/ab >= 6/(a+b)^2
c)(A+a+B+b)/(A+a+B+b+c+d) + (B+b+C+c)/(B+b+C+c+a+d) > (C+c+A+a)/(C+c+A+a+b+d)
a) Cho \(a+b+c+d=2000\) và \(\dfrac{1}{a+b+c}+\dfrac{1}{b+c+d}+\dfrac{1}{c+d+a}+\dfrac{1}{d+a+b}=\dfrac{1}{40}\)
Tính giá trị của: \(S=\dfrac{a}{b+c+d}+\dfrac{b}{c+d+a}+\dfrac{c}{d+a+b}+\dfrac{d}{a+b+c}\)
b) Xác định tổng các hệ số của đa thức \(f\left(x\right)=\left(5-6x+x^2\right)^{2016}\cdot\left(5-6x+x^2\right)^{2017}\)
1. Tìm 4 số a,b,c,d biết rằng:
a. b + c+ d = 1 ; a + c + d = 2 ; a + b + d = 3 ; a + b + c =4
b. a + b + c + d = 1 ; a + c + d = 5 ; a + b + d = 3 ; a + b + c = 6
a. Ta có :
(b + c + d)+(a + c + d)+(a + b + d)+(a + b + c) = 3(a + b + c + d)
⇒3(a + b + c + d)=1+2+3+4=10
⇒a + b + c + d = \(\dfrac{10}{3}\)
⇒a = (a + b + c + d) - (b + c + d) =\(\dfrac{10}{3}\) - 1= \(\dfrac{7}{3}\)
Tương tự ,ta có :
b = \(\dfrac{10}{3}\) - 2= \(\dfrac{4}{3}\) ; c = \(\dfrac{10}{3}\) - 3= \(\dfrac{1}{3}\)
và d = \(\dfrac{10}{3}\) - 4= \(-\dfrac{2}{3}\)
Vậy các số a,b,c,d lần lượt là \(\dfrac{7}{3}\) ;\(\dfrac{4}{3}\) ;\(\dfrac{1}{3}\) và \(-\dfrac{2}{3}\)
Ý b) tương tự như trên.
cho a+b+c+d = 4000 và \(\frac{1}{a+b+c}+\frac{1}{b+c+d}+\frac{1}{c+d+a}+\frac{1}{d+a+b}=\frac{1}{40}\)
tính giá trị của \(S=\frac{a}{b+c+d}+\frac{b}{c+d+a}+\frac{c}{d+a+b}+\frac{d}{a+b+c}\)
Ta có S + 4 = \(\left(\frac{a}{b+c+d}+1\right)+\left(\frac{b}{c+d+a}+1\right)+\left(\frac{c}{a+b+d}+1\right)+\left(\frac{d}{a+b+c}+1\right)\)
\(=\frac{a+b+c+d}{b+c+d}+\frac{a+b+c+d}{a+c+d}+\frac{a+b+c+d}{a+b+d}+\frac{a+b+c+d}{b+c+d}\)
\(=\left(a+b+c+d\right)\left(\frac{1}{b+c+d}+\frac{1}{a+c+d}+\frac{1}{a+b+d}+\frac{1}{a+b+c}\right)\)
\(=4000.\frac{1}{40}=100\)(a + b + c + d = 4000 ; \(\frac{1}{b+c+d}+\frac{1}{a+c+d}+\frac{1}{a+b+d}+\frac{1}{a+b+c}=\frac{1}{40}\))
=> S = 100 - 4 = 96