Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được:
12 15 x 4 y 2 v à 5 9 x y
PB
Những câu hỏi liên quan
Bài 4: Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được:
a) 2 5
x
18
y và 3 2 18x y .
b) 2 2
x
9
y và 36x2 y3
Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được:
- 1 7 x 2 y v à - 2 5 x y 4
Tích của hai đơn thức là:
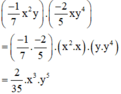
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của x là 3 ; Số mũ của y là 5
⇒ Bậc của đơn thức đó là 3+5=8.
Đúng 1
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được.
1/ - 3x2y và 6x2y3
2/ x3y và 6x2y3
Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được :
a) \(\dfrac{12}{15}x^4y^2\) và \(\dfrac{5}{9}xy\)
b) \(-\dfrac{1}{7}x^2y\) và \(-\dfrac{2}{5}xy^4\)
Hướng dẫn giải:
a) Tích của hai đơn thức 12151215 x4y2 và 5959 xy là 12151215 x4y2 . 5959 xy = 4949 x5 y3;
Đơn thức tích có bậc 8.
b) - 1717 x2y . (-2525 xy4) = 235235 x3y5;
Đơn thức tích có bậc 8.
Đúng 0
Bình luận (1)
a) Tích của hai đơn thức \(\dfrac{12}{15}\)x4y2 và \(\dfrac{5}{9}\) xy là \(\dfrac{12}{15}\) x4y2 . \(\dfrac{5}{9}\) xy = \(\dfrac{4}{9}\) x5 y3;
Đơn thức tích có bậc 8.
b) - \(\dfrac{1}{7}\) x2y . (-\(\dfrac{2}{5}\) xy4) = \(\dfrac{2}{35}\) x3y5;
Đơn thức tích có bậc 8.
Đúng 0
Bình luận (0)
tính tích của các đơn thức sau rồi tìm Bậc của đơn thức thu được:\(\left(\dfrac{-1}{3}x^2y\right)\times\left(6xy^2\right)\)
`(-1/3 x^2 y) .(6xy^2)`
`=(-1/3 . 6).(x^2.x).(y.y^2)`
`=-2 x^3 y^3`
Bậc của đơn thức là `6`
Đúng 6
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được: - 1 3 x 2 y v à 2 x y 3
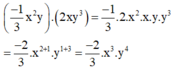
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.
Đúng 0
Bình luận (0)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
1 4 x 3 y v à - 2 x 3 y 5
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12
Đúng 0
Bình luận (0)
BH
19 tháng 4 2022 lúc 19:00
Bài 2: Tính tích của các đơn thức sau, rồi tìm bậc của đơn thức thu được:
a) 2x2y và – 11xy4 ; b) x3y2 và xy5z7
\(a.\left(2x^2y\right).\left(-11xy^4\right)=-22x^3y^5\)
bậc là: 8
\(b.\left(x^3y^2\right).\left(xy^5z^7\right)=x^4y^7z^7\)
bậc là: 18
Đúng 2
Bình luận (1)
`a) ( 2x^2 y ) . ( -11xy^4)`
`= [ 2 . (-11) ] ( x^2 . x ) ( y . y^4 )`
`= -22x^3y^5`
`->` Bậc : `3 + 5 = 8`
`b) ( x^3y^2 ) . ( xy^5z^7 )`
`= ( x^3 . x ) ( y^2 . y^5 ) z^7`
`= x^4y^7z^7`
`->` Bậc: `4 + 7 + 7 = 18`
Đúng 2
Bình luận (0)
Tính tích các đơn thức sau và tìm bậc của đơn thức thu được: 4xy2 và (-3)/4 (x2 y)3
4xy2. [(-3)/4.(x2 y)3]
= 4xy2.[(-3)/4.x6.y3]
= [4.(-3)/4].(x.x6).(y2.y3)
= -3.x7.y5.
Đơn thức có bậc bằng 7 + 5 = 12.
Đúng 0
Bình luận (0)