Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S(2;3;5) và đáy là một đa giác nằm trong mặt phẳng P : 2 x + y − 2 z − 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
PB
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S ( 2 ; 3 ; 5 ) và đáy là một đa giác nằm trong mặt phẳng (P): 2 x + y - 2 z - 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
Đáp án C.
Chiều cao của khối chóp có độ dài bằng d S , P = 2 .
Suy ra thể tích khối chóp đã cho là V = 1 3 . 12 . 2 = 8 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
T
có tâm
I
1
;
3
;
0
ngoại tiếp hình chóp đều
S
.
A
B
C
,
S
A
S
B
S
C
6
, đỉnh
S
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu T có tâm I 1 ; 3 ; 0 ngoại tiếp hình chóp đều S . A B C , S A = S B = S C = 6 , đỉnh S 2 ; 1 ; 2 . Khoảng cách từ S đến mặt phẳng A B C bằng
A. 94 4
B. 11
C. 3
D. 1
Trong không gian với hệ tọa độ Oxyz, cho hình chóp tứ giác đều S.ABCD biết:
A
1
;
0
;
0
,
B
5
;
0
;
0
,
C
5
;
4
;
0
và chiều cao hình chó...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình chóp tứ giác đều S.ABCD biết:
A 1 ; 0 ; 0 , B 5 ; 0 ; 0 , C 5 ; 4 ; 0 và chiều cao hình chóp bằng 6. Gọi I(a,b,c) là điểm cách đều 5 đỉnh của hình chóp (với c > 0). Tính giá trị của T = a + 2 b + 3 c .
A. 41
B. 14
C. 23
D. 32
Trong không gian với hệ tọa độ Oxyz, cho hình chóp
S
.
A
B
C
D
với
S
1
;
-
1
;
6
,
A
1
;
2
;
3
,
B
3
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S . A B C D với S 1 ; - 1 ; 6 , A 1 ; 2 ; 3 , B 3 ; 1 ; 2 , D 2 ; 3 ; 4 . Gọi I là tâm mặt cầu (S) ngoại tiếp hình chóp. Tính khoảng cách d từ I đến mặt phẳng (SAD)
A. d = 6 2
B. d = 21 2
C. d = 3 3 2
D. d = 3 2
Chọn đáp án A
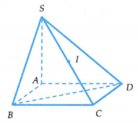
Lấy điểm C trong mặt phẳng (ABD) sao cho ABCD là hình chữ nhật
Do vậy, tâm mặt cầu ngoại tiếp hình chóp là trung điểm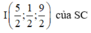 
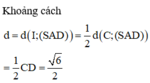
Cách 2: Gọi I(a;b;c) là tâm mặt cầu ngoại tiếp hình chóp là trung điểm S.ABCD. Ta có:
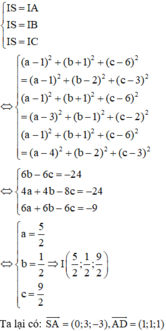
STUDY TIP |
Khi xác định tâm mặt cầu ngoại tiếp hình chop hoặc lăng trụ ta có thể làm theo hai hường: + Hướng 1: Dùng điều kiện tâm cách đều các đỉnh đi đến giải hệ phương trình + Hướng 2: Dựa vào tính đặc biệt của hình như: Hình chop đều, hình chop có các đỉnh cùng nhìn một cạnh dưới một góc vuông |
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;6;0), B(0;6;0), C(0;0;-2). Phương trình mặt cầu ngoại tiếp hình chóp OABC (O là gốc tọa độ) là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;6;0), B(0;6;0), C(0;0;-2). Phương trình mặt cầu ngoại tiếp hình chóp OABC (O là gốc tọa độ) là:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;6;0), B(0;6;0), C(0;0;-2). Phương trình mặt cầu ngoại tiếp hình chóp OABC (O là gốc tọa độ) là: A.
x
+
1
2
+
y
-
3
2
+
z
+
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2;6;0), B(0;6;0), C(0;0;-2). Phương trình mặt cầu ngoại tiếp hình chóp OABC (O là gốc tọa độ) là:
A. x + 1 2 + y - 3 2 + z + 1 2 = 11
B. x + 1 2 + y - 3 2 + z + 1 2 = 11
C. x + 1 2 + y - 3 2 + z + 1 2 = 44
D. x + 1 2 + y - 3 2 + z + 1 2 = 91
Chọn A
Tâm I của mặt cầu là trung điểm của AC
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho S(1;2;3) và các điểm A , B , C thuộc các trục Ox ,Oy , Oz sao cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Thể tích khối chóp S.ABC là?
☺☻♥♦♣♠•◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓→←2◘↔▲▼ !"#◘%&'Ü)*+,-./0123;
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp. A. A’(-3;2;1) B. A’(-3;-3;3) C. A’(-3;-3;-3) D. A’(-3;3;3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B’(-2;1;1), D’(3;5;4). Tìm tọa độ điểm A’ của hình hộp.
A. A’(-3;2;1)
B. A’(-3;-3;3)
C. A’(-3;-3;-3)
D. A’(-3;3;3)
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’. Biết tọa độ các đỉnh A(-3;2;1), C(4;2;0), B'(-2;1;1), D'(3;5;4). Tìm tọa độ điểm A’ của hình hộp
A. A'(-3;3;1)
B. A'(-3;-3;3)
C. A'(-3;-3;-3)
D. A'(-3;3;3)
