Ba người thợ săn cùng bắn vào 1 con thú với khả năng bắn trúng tương ứng là 0,4; 0,5 và 0,7. Tính
a) Xác suất để con thú bị trúng ít nhất 1 viên đạn
b) Biết rằng con thú bị trúng ít nhất 1 viên đạn, tính xác suất để người thợ săn thứ 2 bắn trúng
Có ba người đi săn cung bắn 1 cách độc lập vào 1 con thú vào cùng 1 thời điểm. Xác xuất bắn trúng mục tiêu của ba người lần lượt là 0,5;0,6;0,7. tính xác xuất để con thú bị bắn trúng
Ta có : \(\overline{A}=\overline{A_1UA_2UA_3}=\overline{A_1}\) \(\overline{A_2}\)\(\overline{A_3}\)= sự kiện không có ai bắn trúng
\(\Rightarrow P\left(\overline{A}\right)=\)\((\overline{A_1}\)\(\overline{A_2}\)\(\overline{A_3})\)\(=P\left(\overline{A_1}\right)P\left(\overline{A_2}\right)P\left(\overline{A_3}\right)=0,5.0,4.0,3=0,06\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-0,06=0,94\)
Vậy xác xuất để con thú bị bắn trúng là 0,94
Ba người A, B, C đi săn độc lập với nhau, cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng là 0,7; 0,6; 0,5. Xác suất để có ít nhất một người bắn trúng là:
![]()
![]()
![]()
![]()
Ba người A, B, C đi săn độc lập với nhau, cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng là 0,7; 0,6; 0,5. Xác suất để có ít nhất một người bắn trúng là:
A. 0,94
B. 0,8
C. 0,45
D. 0,75
Chọn A.
Phương pháp:
Áp dụng quy tắc cộng và nhân xác suất.
Cách giải:
Xác suất để có ít nhất một người bắn trúng là:
1 − 1 − 0 , 7 1 − 0 , 6 1 − 0 , 5 = 1 − 0 , 3.0 , 4.0 , 5 = 0 , 94
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?
A. 0,75
B. 0,45
C. 0,94
D. 0,80
Đáp án C
Gọi X ¯ là biến cố
Không một xạ thủ nào bắn trúng
![]()
Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau
Suy ra P ( X ¯ ) = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06
![]()
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?
A. 0,75
B. 0,45
C. 0,94
D. 0,80
Đáp án C
Gọi X ¯ là biến cố: Không một xạ thủ nào bắn trúng. Khi đó X ¯ = A ¯ ∪ B ¯ ∪ C ¯ . Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau.
Suy ra P X ¯ = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06 ⇒ P X ¯ = 1 - P X ¯ = 0 , 94 .
Một thợ săn bắn 3 viên đạn vào con mồi. Xác suất để bắn viên đạn trúng mục tiêu là 0,3.
c) Xác suất để người thợ săn có 2 viên bắn trúng mục tiêu:
A. 0,063
B. 0,189
C. 0,147
D. 0,09
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
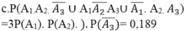
Chọn B
Một thợ săn bắn 3 viên đạn vào con mồi. Xác suất để bắn viên đạn trúng mục tiêu là 0,3.
b) xác suất để người thợ săn bắn trúng mục tiêu ở viên thứ 3 là:
A. 0,147
B. 0,27
C. 0,343
D. 0,973
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
![]()
Chọn A
Một thợ săn bắn 3 viên đạn vào con mồi. Xác suất để bắn viên đạn trúng mục tiêu là 0,3.
a) Xác suất để người thợ săn bắn trượt mục tiêu là:
A. 0,7
B. 0,27
C. 0,343
D. 0,973
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
![]()
Chọn C
Ba người cùng bắn vào một bia, mỗi người bắn một viên. Xác suất bắn trúng bia
của người thứ nhất, thứ hai, thứ ba tương ứng là 0,1;0,2;0,3. Gọi Ai là biến cố “
người thứ i bắn trúng bia”, i=1,2,3. Tính xác suất xảy ra các tình huống sau.
a. Chỉ có người thứ nhất bắn trúng.
b. Có ít nhất một người bắn trúng.
c. Cả ba người cùng bắn trúng bia.
d. Người đầu bắn trúng, người thứ hai bắn trượt.
e. Có đúng một người bắn trúng.
f. Có ít nhất hai người bắn trúng.
g. Có không quá hai người bắn trúng
Lời giải:
a. Xác suất chỉ người thứ nhất bắn trúng là:
$0,1(1-0,2)(1-0,3)=0,056$
b. Xác suất không người nào bắn trúng: $(1-0,1)(1-0,2)(1-0,3)=0,504$
Xác suất có ít nhất 1 người bắn trúng: $1-0,504=0,496$
c. Xác suất cả 3 người bắn trúng: $0,1.0,2.0,3=0,006$
d.
Xác suất người đầu bắn trúng và người 2 trượt:
$0,1(1-0,2)=0,08$
e.
Xác suất có đúng 1 người bắn trúng:
$0,1(1-0,2)(1-0,3)+(1-0,1).0,2.(1-0,3)+(1-0,1)(1-0,2)0,3=0,398$
f. Xác suất có ít nhất 2 người bắn trúng:
1- xác suất cả 3 cùng trượt - xác suất chỉ có 1 người bắn trúng
= $1-(1-0,1)(1-0,2)(1-0,3)-0,398=0,098$
g.
Xác suất không có quá 2 người bắn trúng
= 1- xác suất cả 3 người trúng = $1-0,1.0,2.0,3=0,994$