Giải phương trình cos2x + 5sinx - 4 = 0
![]()
![]()
![]()
![]()
Giải phương trình cos 2 x + 5 sin x - 4 = 0 .
A. x = π 2 + k π
B. x = - π 2 + k π
C. x = k 2 π
D. x = π 2 + k 2 π
Đáp án D
Phương trình
cos 2 x + 5 sin x - 4 = 0 ⇔ 1 - 2 sin 2 x + 5 sin x - 4 = 0 ⇔ 2 sin 2 x - 5 sin x + 3 = 0 ⇔ 2 sin x - 3 sin x - 1 = 0 ⇔ sin x = 1 ⇔ x = π 2 + k 2 π k ∈ ℤ
Giải phương trình cos 2 x + 5 sin x - 4 = 0
![]()
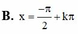
![]()
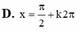
Giải phương trình cos 2 x + 5 sin x - 4 = 0
A. x = π 2 + k π
B. x = - π 2 + k π
C. x = k 2 π
D. x = π 2 + k 2 π
Giải phương trình cos2x + 5sinx-4 = 0
A. 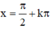
B. 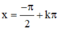
C. ![]()
D. ![]()
Giải phương trình sin2x-cos2x+5sinx-cosx-2=0
<=> (2sinxcosx-cosx)+5sinx-2-cos2x=0
<=> cosx(2sinx-1)+2\(sin^2x\)+5sinx-3=0
<=> cosx(2sinx-1) +(2sinx-1)(sinx+3)
<=> (2sinx-1)(cosx+sinx+3)=0
<=>\(\begin{cases}sinx=\frac{1}{2}\\cosx+sinx+3=0\end{cases}\)
+) sinx=1/2
<=> \(x=\frac{\pi}{2}+k2\pi\) với k thuộc Z
+) cosx+sinx+3= <=>\(\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)=-3
<=> \(sin\left(x+\frac{\pi}{4}\right)\)=\(\frac{-\sqrt{3}}{2}\)
<=>\(sin\left(x+\frac{\pi}{4}\right)=sin\frac{-\pi}{3}\)
<=> \(\left[\begin{array}{nghiempt}x=\frac{-\pi}{3}+k2\pi\\x=\frac{4\pi}{3}+k2\pi\end{array}\right.\)với k thuộc Z
vậy pht có 3 nghiệm:..
Giải phương trình 5 sinx + sin 3 x + cos 3 x 1 + 2 sin 2 x = cos 2 x + 3
A. x = ± π 3 + k2π .
B. x = ± π 6 + k2π, k ∈ Z
C. x = ± π 3 + kπ
D. x = ± π 6 + kπ, k ∈ Z
Nghiệm của phương trình c o s 2 x − 5 sin x − 3 = 0 là:
A. x = − π 6 + k 2 π x = 7 π 6 + k 2 π , k ∈ ℤ .
B. x = − π 3 + k 2 π x = 7 π 3 + k 2 π , k ∈ ℤ .
C. x = − π 6 + k π x = 7 π 6 + k π , k ∈ ℤ .
D. x = − π 3 + k π x = 7 π 3 + k π , k ∈ ℤ .
Đáp án A
P T ⇔ 1 − 2 sin 2 x − 5 sin x − 3 ⇔ 2 sin 2 x + 5 sin x + 2 = 0 ⇔ sin x = − 1 2 sin x = − 2
⇒ sin x = − 1 2 ⇔ x = − π 6 + k 2 π x = 7 π 6 + k 2 π k ∈ ℤ
Tổng các nghiệm của phương trình cos 2 x + 5 sin x - 3 = 0 trên khoảng 0 ; 10 π
A. 28 π
B. 45 π
C. 25 π
D. 66 π
Tổng các nghiệm của phương trình cos 2 x + 5 sin x - 3 = 0 trên khoảng 0 ; 10 π bằng
A. 28 π
B. 45 π
C. 25 π
D. 66 π