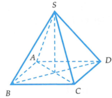
Hình chóp đều S.ABCD tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình chóp là:
Đọc tiếp
Hình chóp đều S.ABCD tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình chóp là:
PB
Những câu hỏi liên quan
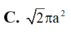
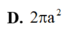
Hình chóp đều S.ABCD tất cả các cạnh bằng a. Diện tích mặt cầu ngoại tiếp hình chóp là:
A. 4 πa 2
B. πa 2
C. 2 πa 2
D. 2 πa 2
Đáp án D
Gọi O là tâm của hình vuông ABCD ta có:
Đúng 0
Bình luận (0)
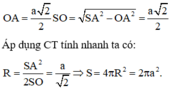
Hình chóp đều S.ABCD tất cả các cạnh bằng a . Diện tích mặt cầu ngoại tiếp hình chóp là:
A. 4 πa 2
B. πa 2
C. 2 πa 2
D. 2 πa 2
Chọn đáp án D
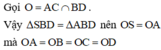
Suy ra, O cách đều tất cả các đỉnh của hình chóp.
Suy ra, O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Bán kính mặt cầu này
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Thể tích khối cầu ngoại tiếp hình chóp là A.
8
πa
3
2
B.
8
πa
3
2
3
C.
4
πa
3
2
3...
Đọc tiếp
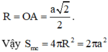
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Thể tích khối cầu ngoại tiếp hình chóp là
A. 8 πa 3 2
B. 8 πa 3 2 3
C. 4 πa 3 2 3
D. πa 3 2 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Thể tích của khối cầu ngoại tiếp hình chóp đã cho bằng
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Thể tích của khối cầu ngoại tiếp hình chóp đã cho bằng
Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a có diện tích là: A. S
4
πa
2
B. S
2
2
πa
2
C. S
2
πa
2
D. S
3
πa
2
2
Đọc tiếp
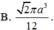
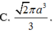
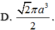
Mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a có diện tích là:
A. S = 4 πa 2
B. S = 2 2 πa 2
C. S = 2 πa 2
D. S = 3 πa 2 2
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó ?
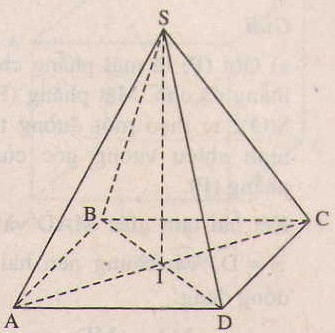
Gọi I = AC ∩ BD. Ta thấy AC = a√2 = BD,
SA = SC = a, nên SA2 + SC2 = AC2. Vậy điểm S nhìn AC dưới một góc vuông. Các điểm B và D cũng nhìn AC dưới một góc vuông.
Vậy mặt cầu ngoại tiếp hình chóp là mặt cầu đường kính AC. Tâm của cầu là điểm I và bán kính R =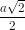 
. Ta thấy rằng điểm I cũng là chân đường cao hạ từ đỉnh S xuống đáy.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho. A.
R
a
3
2
B.
R
a
2
4
C.
R
a
2
D.
R
a...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
A. R = a 3 2
B. R = a 2 4
C. R = a 2
D. R = a 2 2
Chọn C.
Phương pháp:
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều.
Cách giải:
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a A.
2
πa
2
3
B.
2
πa
2
C.
4
πa
2
3
D.
4
πa
2
Đọc tiếp
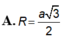
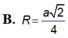
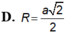
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh bằng a
A. 2 πa 2 3
B. 2 πa 2
C. 4 πa 2 3
D. 4 πa 2
