Một hình nón có đường sinh bằng a, góc ở đỉnh bằng 120 o . Tính thể tích V của hình nón
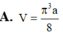
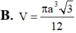
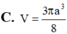
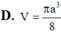
Một hình nón tròn xoay có góc ở đỉnh bằng 120 o , đường sinh bằng a. Tính thể tích V của hình nón
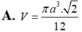
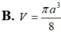
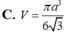
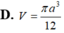
Biết hình nón có góc ở đỉnh bằng 120 o , đường sinh bằng a. Tính thể tích V của hình nón theo a.
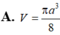

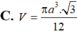
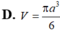
Cho hình nón (N) có đỉnh O, góc ở đỉnh bằng 120 ° , độ dài đường sinh bằng a. Mặt phẳng qua O cắt hình nón theo một thiết diện có diện tích lớn nhất bằng
A. 3 a 2 4
B. a 2 4
C. 3 a 2 2
D. a 2 2
Một hình nón có đường sinh bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120 ° . Thể tích của khối nón bằng
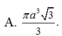
![]()
![]()
![]()
Biết góc ở đỉnh của một hình nón xoay bằng 120 o , độ dài đường sinh bằng a. Tính thể tích V của hình tròn
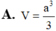
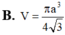
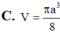
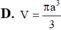
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
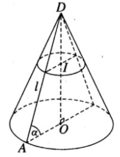
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos α (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: S xq = πrl = πl 2 cosα
Khối nón có chiều cao h = DO = lsin α . Do đó thể tích V của khối nón được tính theo công thức
![]()
Vậy :
![]()
Cho hình nón tròn xoay có độ dài đường sinh là 2a , góc ở đỉnh của hình nón bằng 60 ° . Thể tích V của khối nón đã cho là
A. V = πa 3 3
B. V = π 3 a 3
C. V = π a 3
D. π 3 a 3 3
Cho hình nón tròn xoay có độ dài đường sinh là 2a, góc ở đỉnh của hình nón bằng 60 ° . Thể tích V của khối nón đã cho là
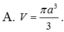
![]()
![]()
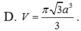
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S xq của hình nón và thể tích V của khối nón tương ứng là:
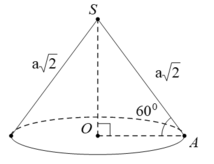
A. S xq = πa 2 ; V = πa 3 6 12
B. S xq = πa 2 2 ; V = πa 3 3 12
C. S xq = πa 2 2 ; V = πa 3 6 4
D. S xq = πa 2 ; V = πa 3 6 4
Đáp án A
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là SAO ^ = 60°.
