Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
PB
Cho tam giác ABC cân tại A, góc B A C ^ 120 o và AB 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
Đọc tiếp
Lớp 12 Toán
Những câu hỏi liên quan
PB
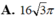
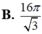
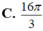
Cho tam giác ABC cân tại A, góc B A C ^ 120 °  và AB4cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC A.  16 3 π B.  16 π 3 C.  16...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
CT
1 tháng 10 2019 lúc 14:07

Chọn đáp án D

Phương pháp

Sử dụng công thức tính thể tích khối nón có chiều cao h và bán kính đáy r là

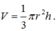
Cách giải

Áp dụng định lí cosin trong tam giác ABC ta có:

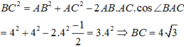
+) Gọi H là trung điểm của BC.

Khi quay tam giác ABC quanh cạnh BC ta được 2 hình nón có chung bán kính đáy AH, đường cao lần lượt là BH và CH với

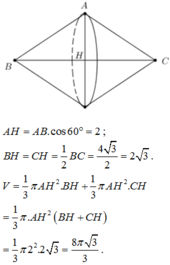
+) Khi quay tam giác ABC quanh AB ta được khối tròn xoay như sau:

Gọi D là điểm đối xứng C qua AB, H là trung điểm của CD

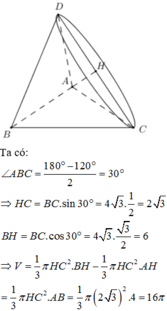
+) Do điểm B và C có vai trò như nhau nên khi quay tam giác ABC quanh AC ta cũng nhận được khối tròn xoay có thể tích bằng 16.

Vậy thể tích lớn nhất có thể được khi quay tam giác ABC quanh một đường thẳng chứa cạnh của tam giác ABC là 16π

Bình luận (0)
LT

Cho tam giác ABC cân tại A, AB= 4cm. Góc BAC = 120 độ. Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC?

Xem chi tiết
Lớp 9 Toán Câu hỏi của OLM

Khách
 
H24
17 tháng 6 2019 lúc 21:49

Gọi đường tròn (O; R) là đường tròn ngoại tiếp tam giác ABC.


Kẻ đường kính AO cắt (O) tại D.

Hai tam giác vuông ABH và ADC có ∠ABH =∠ADC (cùng chắn cung AC) nên chúng đồng dạng.

=>ABAD=AHAC=>ABAD=AHAC

=>AD=AB⋅ACAH=6⋅103=20(cm)=>AD=AB⋅ACAH=6⋅103=20(cm)

Do đó, R=AD2=202=10(cm)

P.s:Ko chắc 

Bình luận (0)
CN

cho tam giác abc cân tại a có bc = 6cm đg cao ah =4cm h thuộc bc 2đg trung trực của ab và ac cắt nhau tại o

a) tính ab ,ac so sánh các góc trong tam giác abc

b)cm 3đ a,o,h thẳng hàng và oa=ob=oc

c)cmr om =on

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
LS

Cho tam giác ABC có góc A 120​o. Một đường thẳng qua A cắt BC tại D, chia tamgiác ABC thành hai tam giác cân. Tính số đo các góc B và C của tam giác ABC.

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
TH

cho tam giác ABC cân tại A, tia phân giác của B và C cắt nhau tại O, cắt AC và AB lần lượt tại D và E.

a.   Chứng minh BD=CE

b.   Vẽ OH vuông góc với AB, OK vuông góc với AC,OI vuông góc với BC. Chứng minh: OH=OI và tam giác HOK cân

c.   Gỉa sử góc BAC =120 độ, tính các góc của tam giác OHK

 

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
H24
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, widehat{BAC}120^o, ABACa. Tam giác SAB vuông tại B, tam giác SAC vuông tại C, góc giữa hai mặt phẳng left(SABright) và left(ABCright) bằng 60^o. Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng left(ABCright). Chứng minh rằng HB vuông góc AB và tính thể tích khối chóp S.ABC theo a
Đọc tiếp
Xem chi tiết
Lớp 12 Toán Chương 1: KHỐI ĐA DIỆN

Khách
 
QH

Cho tam giác ABC cân tại A,các tia phân giác góc b và góc c cắt nhau ở O,cắt AC và AB lần lượt ở D và E

a)CM BD=CE

b)Vẽ OH vuông góc với QB ,OK vuông góc với AC,OI vuông góc với BC.CM OH= OI mà tam giác OMK cân

c )Giả sử gíc BAC=120. Tính các góc tam giác OHK

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
SY
16 tháng 8 2019 lúc 11:57

a, xét 2 tam giác EBC và tam giác DBC ta có:

góc DBC = góc ECB (vì ABC cân )

góc EBC = DCB (abc cân)

bc chung

=> 2 tam giác bằng nhau => BD = CE ( đpcm)

b, xét tam giác BHO và BIO ta có:

góc H=I (=90độ)

góc HBO=OBI(phân giác)

BO chung 

=>2 tam giác = nhau => HO=OI (đpcm) 

xét 2 tam giác ABO và ACO ta có: (bạn tự làm nha ) 

=> 2 tam giác = nhau (c-g-c) => HO=OK

=> tam giác OHK cân

p/s: mình nghĩ bạn nên kiểm tra lại trước khi đăng, chứ câu b và câu c mình thấy sai sai và cũng không hiểu để làm )

Bình luận (0)
PD

cho tam giác ABC cân tại A ; góc a = 120 độ   b) Tính góc B,góc C  b) Vẽ Bx vuông dóc với AB và Cy vuông góc vs AC, Bx cắt Cy tại E. Chứng minh tam giác BCD đều

Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách
 
TS

Bài 1: Cho tam giác ABC vuông tại A, tanB=3\4, AB=4cm. Giải tam giác?

Bài 2 : Cho tam giác ABC cân tại A, góc BAC=42, AB=AC=7cm,

a Đường cao AH=?

b BC=?

c Đường cao CK=?

Bài 3: Cho tam giác ABC cân tại A, AB=AC=8,5cm, BC=8cm.

a Tính các góc của tam giác ABC?

b Diện tích của tam giác ABC=?

giải từng bước...

Xem chi tiết
Lớp 9 Toán Câu hỏi của OLM

Khách
 
H24
1) Vẽ tam giác ABC đều có cạnh là 3 cm . Vẽ điểm D sau B là trung điểm của CD tính số đo các góc của tam giác ABD2) Vẽ tam giác ABC cân tại B có góc B 50o và AB 4cm. Nêu cách vẽ. Tính số đo còn lại của tam giác đó3) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC)a) Chứng minh HB HC b) Chứng minh góc BAH góc CAHc) Kẻ HD thuộc AB ( D thuộc AB)    Kẻ HE thuộc AC (E thuộc AC)Chứng minh tam giác HDE là tam giác cân
Đọc tiếp
Xem chi tiết
Lớp 7 Toán Câu hỏi của OLM

Khách