Cho số phức z = 3 -5i. Phần ảo của z là
A. -5
B. -5i
C. 5
D. 3
Cho số phức z = 3 − 5 i . Phần ảo của z là
A. − 5.
B. − 5 i .
C. 5.
D. 3.
Đáp án A
Cho số phức z = x + y i với x , y ∈ R .
Khi đó y được gọi là phần ảo của z.
Vậy - 5 là phần ảo của số phức z = 3 − 5 i .
Tìm phần thực và phần ảo của số phức z, biết z ¯ = 5 + i 2 1 − 5 i
A. Phần thực bằng -14 và phần ảo bằng 2 5
B. Phần thực bằng 14 và phần ảo bằng 2 5 i
C. Phần thực bằng 14 và phần ảo bằng 2 5
D. Phần thực bằng -14 và phần ảo bằng 2 5 i
Đáp án C
Ta có:
z ¯ = 4 + 2 i 5 1 − i 5 = 14 − 2 i 5 ⇒ z = 14 + 2 i 5
Do đó số phức z có phần thực bằng 14 và phần ảo bằng 2 5
Tìm phần thực và phần ảo của số phức z, biết z ¯ = ( 5 + i ) 2 ( 1 - 5 i )
A. Phần thực bằng -14 và phần ảo bằng 2 5
B. Phần thực bằng 14 và phần ảo bằng 2 5 i
C. Phần thực bằng 14 và phần ảo bằng 2 5
D. Phần thực bằng -14 và phần ảo bằng 2 5 i
Đáp án C
Ta có ![]()
![]()
Do đó số phức z có phần thực bằng 14 và phần ảo bằng 2 5
Phần ảo của số phức z=4+5i là
A. 5i.
B. 4.
C. 5.
C. 4i.
Trong các số phức z thỏa mãn z − 5 i ≤ 3 , số phức có z nhỏ nhất có phần ảo bằng bao nhiêu?
A. 4
B. 0
C. 3
D. 2
Đáp án D
Gọi M là điểm biểu diễn của số phức z trong mặt phẳng tọa độ.
Từ z − 5 i ≤ 3 suy ra tập hợp điểm M là hình tròn có tâm I(0;5), bán kính R = 3.
Vì z = OM nên số phức z có môđun nhỏ nhất là z = 2i ứng với điểm M 1 0 ; 2 .
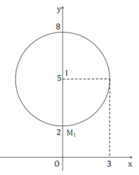
Trong các số phức z thỏa mãn |z-5i| ≤ 3, số phức có |z| nhỏ nhất có phần ảo bằng bao nhiêu?
A. 4.
B. 0.
C. 3.
D. 2
Đáp án D
Gọi M là điểm biểu diễn của số phức z trong mặt phẳng tọa độ.
Từ |z-5i| ≤ 3 suy ra tập hợp điểm M là hình tròn có tâm I(0;5), bán kính R = 3.
Vì |z| + OM nên số phức z có môđun nhỏ nhất là z = 2i ứng với điểm M 1 (0;2).
Phần thực và phần ảo của số phức z=1-5i là
A. -5 và 1.
B. 1 và -5.
C. 1 và -5i.
D. 1 và 5.
Cho hai số phức z 1 = 1-3i và z 2 = -2-5i . Tìm phần ảo b của số phức z = z 1 - z 2
A. b = -2
B. b = 2
C. b = 3
D. b = -3
Tìm phần thực, phần ảo, số phức liên hợp, tính muđon của số phức z. biết z thõa mãn: 10z + 2i
– 3 = (4 – 5i)z + 3i
Đặt $z=a+bi$ ( $a,b\in\mathbb{R}$)
Theo bài ra ta có:
\(10(a+bi)+2i-3=(4-5i)(a+bi)+3i\Leftrightarrow (6a-5b-3)+i(6b-1+5a)=0\)
\(\Rightarrow \left\{\begin{matrix} 6a-5b-3=0\\ 5a+6b-1=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{23}{61}\\ b=\frac{-9}{61}\end{matrix}\right.\). Do đó số \(z=\frac{23}{61}-\frac{9i}{61}\)
Vậy:
-Phần thực: $a=\frac{23}{61}$
-Phần ảo: $b=\frac{-9}{61}$
-Số phức liên hợp \(\overline{z}=a-bi=\frac{23}{61}+\frac{9i}{61}\)
-Mô đun: \(|z|=\sqrt{a^2+b^2}=\frac{\sqrt{610}}{61}\)