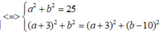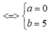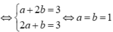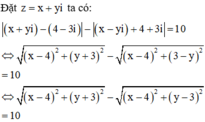Cho số phức z thỏa mãn z-(1+3i) z ¯ = -3+8i. Tính |z|.
PB
Những câu hỏi liên quan
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i
Cho số phức z thỏa mãn
z
-
1
-
i
1
, số phức w thỏa mãn
w
¯
-
2
-
3
i
2
. Tính giá trị nhỏ nhất của
z
-
w...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Cho số phức z thỏa mãn
5
z
+
i
5
-
i
z
biết rằng tập hợp điểm biểu diễn cho số phức w thỏa mãn
w
(
1
-
i
)
(
6
-
8
i
)
z
+
3
i
+
2
là một đường tròn. Xác định tọa độ tâm I của đường...
Đọc tiếp
Cho số phức z thỏa mãn 5 z + i = 5 - i z biết rằng tập hợp điểm biểu diễn cho số phức w thỏa mãn w ( 1 - i ) = ( 6 - 8 i ) z + 3 i + 2 là một đường tròn. Xác định tọa độ tâm I của đường tròn đó.
A. I(-1;5)
B. I (1; -5)
C. I = ( - 1 2 ; 5 2 )
D. I = ( 1 2 ; - 5 2 )
Cho số phức z thỏa mãn
z
-
4
+
3
i
-
z
¯
+
4
+
3
i
10
và
z
-
3
-
4
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 4 + 3 i - z ¯ + 4 + 3 i = 10 và z - 3 - 4 i nhỏ nhất. Môđun của số phức z bằng
A. 6
B. 7
C. 5
D. 8
Cho số phức z a + bi (a,b
∈
ℝ
) thỏa mãn z + 2i
z
¯
3 + 3i. Tính z. A. |z| 2 B. |z|
5
C. |z| 5 D. |z|
2
Đọc tiếp
Cho số phức z = a + bi (a,b ∈ ℝ ) thỏa mãn z + 2i z ¯ = 3 + 3i. Tính z.
A. |z| = 2
B. |z| = 5
C. |z| = 5
D. |z| = 2
Cho số phức z thỏa mãn
z
+
1
-
i
z
-
3
i
. Tính môđun lớn nhất
w
m
a
x
của số phức
w
1
2
A.
w...
Đọc tiếp
Cho số phức z thỏa mãn z + 1 - i = z - 3 i . Tính môđun lớn nhất w m a x của số phức w = 1 2
A. w m a x = 7 5 10
B. w m a x = 2 5 7
C. w m a x = 4 5 7
D. w m a x = 9 5 10
Cho số phức z thỏa mãn:
z
-
4
+
3
i
-
z
¯
+
4
-
3
i
10
và
z
-
3
-
4
i...
Đọc tiếp
Cho số phức z thỏa mãn: z - 4 + 3 i - z ¯ + 4 - 3 i = 10 và z - 3 - 4 i nhỏ nhất. Mô đun của số phức z bằng:
A. 6
B. 7
C. 5
D. 8
Cho số phức z thỏa mãn: z − 2 z ¯ = − 7 + 3 i + z . Tính z .
A. 3
B. 13 4
C. 25 4
D. 5
Đáp án D
Đặt z = a + b i a ; b ∈ ℝ ta có:
a 2 + b 2 − 2 a − b i = − 7 + 3 i + a + b i
⇔ a 2 + b 2 = 3 a − 7 + 3 i − b i ⇔ a 2 + b 2 = 3 a − 7 b = 3 ⇔ a 2 + 9 = 3 a − 7 1 b = 3
Lại có:
1 ⇔ a ≥ 7 3 a 2 + 9 = 9 a 2 − 42 a + 49 ⇔ a = 4 ⇒ z = 5
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
+
1
-
i
z
-
3
i
. Tính môđun nhỏ nhất của z - i. A.
3
5
10
B.
4
5
5...
Đọc tiếp
Cho số phức z thỏa mãn z + 1 - i = z - 3 i . Tính môđun nhỏ nhất của z - i.
A. 3 5 10
B. 4 5 5
C. 3 5 5
D. 7 5 10