Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z, thỏa mãn điều kiện
z
2
là một số ảo.
Đọc tiếp
Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z, thỏa mãn điều kiện z 2 là một số ảo.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z, thỏa mãn điều kiện
z
2
là một số ảo A. Hai đường thẳng
y
±
x
(trừ gốc tọa độ O) B. Trục tung (trừ gốc tọa độ O) C. Đường tròn
x
2
+
y
2
1
D. Trục hoành (trừ gốc tọa độ O)
Đọc tiếp
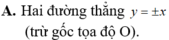
Tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z, thỏa mãn điều kiện z 2 là một số ảo
A. Hai đường thẳng y = ± x (trừ gốc tọa độ O)
B. Trục tung (trừ gốc tọa độ O)
C. Đường tròn x 2 + y 2 = 1
D. Trục hoành (trừ gốc tọa độ O)
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần thực của z là số đối của phần ảo của nó
Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần thực của z bằng phần ảo của nó
Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện: Phần ảo của z bằng -2
Phần ảo của z bằng -2
⇔ y = -2
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng y = -2.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện: Phần ảo của z bằng hai lần phần thực của nó cộng với 1
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z
-
(
3
-
4
i
)
2
A. Đường tròn tâm I(3;4) R12 B. Đường tròn tâm I(3;4) R4 C. Đường tròn tâm I(3;-4) R2 D. Đường tròn tâm I(3;...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện z - ( 3 - 4 i ) = 2
A. Đường tròn tâm I(3;4) R=12
B. Đường tròn tâm I(3;4) R=4
C. Đường tròn tâm I(3;-4) R=2
D. Đường tròn tâm I(3;4) R=8
Chọn C.
Đặt 
;
suy ra 
Từ giả thiết, ta có:
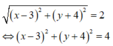
Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(3;-4) bán kính R=2.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
z
-
3
-
4
i
2
. A. Đường tròn tâm
I
3
;
4
R...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện z - 3 - 4 i = 2 .
A. Đường tròn tâm I 3 ; 4 R = 12
B. Đường tròn tâm I 3 ; 4 R = 4
C. Đường tròn tâm I 3 ; - 4 R = 2
D. Đường tròn tâm I 3 ; 4 R = 8
Xét các số phức z thỏa mãn điều kiện
z
-
1
+
i
2
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w z + 2 -i là A. đường tròn tâm I(-3;2), bán kính R 2. B. đường tròn tâm I(3;-2), bán kính R 2. C. đường tròn tâm I(1;0), bán kính R 2. D. đường tròn tâm I(1;-1), bán kính R 2.
Đọc tiếp
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
Ta có: | 2 + z | 2 < | 2 - z | 2
⇔ | 2 + x + iy | 2 < | 2 - x - iy | 2
⇔ 2 + x 2 + y 2 < 2 - x 2 + - y 2
⇔ x < 0
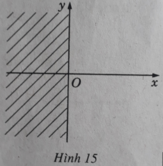
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.
Đúng 0
Bình luận (0)