Cho số thực dương a. Biểu thức thu gọn của biểu thức P = a 4 3 a - 1 3 + a 2 3 a 1 4 a 3 4 + a - 1 4 là:
A. 1
B. a + 1
C. 2a
D. a
PB
Những câu hỏi liên quan
Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Đọc tiếp
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó. A.
2
1009
B.
1
1009
C.
3
1009
D.
3...
Đọc tiếp
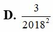
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A. 2 1009
B. 1 1009
C. 3 1009
D. 3 2018 2
Cho số thực dương a. Rút gọn biểu thức
4
a
-
9
a
-
1
2
a
1
2...
Đọc tiếp
Cho số thực dương a. Rút gọn biểu thức 4 a - 9 a - 1 2 a 1 2 - 3 a - 1 2 + a - 4 + 3 a - 1 a 1 2 - a - 1 2
A. 9 a 1 2
B. 9a
C. 3a
D. 3 a 1 2
4
a
-
9
a
-
1
2
a
1
2
-
3
a
-
1
2
+
a
-
4
+
3
a
-
1
a
1
2
-
a
-
1
2
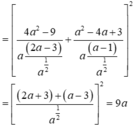
Chọn B
Đúng 0
Bình luận (0)
Cho số thực dương a . Rút gọn biểu thức
a
a
a
a
:
a
11
6
A.
a
3
4
B.
a
1
2
C. a D.
a
1
4
Đọc tiếp
Cho số thực dương a . Rút gọn biểu thức a a a a : a 11 6
A. a 3 4
B. a 1 2
C. a
D. a 1 4
Cho biểu thức: B = (2x+5)2 – (3-x)(3+x) + 14
a) Thu gọn biểu thức B
b) Chứng minh giá trị của biểu thức B luôn luôn dương với mọi giá trị của biến x.
Cho biểu thức: B = (2x+5)2 – (3-x)(3+x) + 14
a) Thu gọn biểu thức B
b) Chứng minh giá trị của biểu thức B luôn luôn dương với mọi giá trị của biến x.
\(a,B=4x^2+20x+25-9+x^2+14=5x^2+20x+30\\ b,B=5\left(x^2+4x+4\right)+10\\ B=5\left(x+2\right)^2+10\ge10>0,\forall x\)
Do đó B luôn dương với mọi x
Đúng 0
Bình luận (0)
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6 .
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Đáp án B.
Ta có A = a 1 3 b + b 1 3 a a 6 + b 6 = a 1 3 b 1 3 b 6 + a 6 a 6 + b 6 = a 1 3 b 1 3 = a b 3 .
Đúng 0
Bình luận (0)
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+
b
6
A.
A...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+
b
6
....
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6 .
A. A = a b 6
B. A = a b 3
C. 1 a b 3
D. 1 a b 6
Đáp án B
Sử dụng máy tính tính giá trị của A với a=2;b=3 rồi lưu vào biến X:
Với A:
Kết quả ra khác 0 nên ta loại A.
Với B:
Vậy ta chọn B.
Đúng 0
Bình luận (0)