\(x^3+3x^2=-3x-1\)

\(\Leftrightarrow x^3+3x^2+3x+1=0\)

\(\Leftrightarrow\left(x+1\right)^3=0\)

\(\Leftrightarrow x+1=0\)

\(\Leftrightarrow x=-1\)

(1-3x²)-(x-2)(9x+1)=(3x-4)(3x+4)-9(x+3)²

⇒1-3x²-(9x²+x-18x-2)=9x²-16-9(x²+6x+9)

⇒1-3x²-(9x²-17x-2)= -56x-97

⇒1-3x²-9x²+17x+2=-56x-97

⇒3-12x²+17x=-56x-97

⇒3-12x²+17x+56x+97=0

⇒-12x²+73x+100=0

⇒-(12x²-73x-100)=0

Ta có

x 3   +   3 x 2   +   3 x   +   1   =   0   ⇔   ( x   +   1 ) 3   =   0

ó x + 1 = 0 ó x = -1

Vậy x = -1

Đáp án cần chọn là: A

Bài 1.

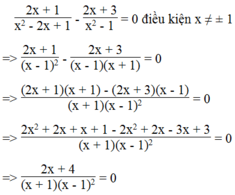
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0

Ta có: 2x + 4 = 0 => x = - 2 (thỏa mãn điều kiện)

Vậy với x = - 2 thì giá trị của biểu thức bằng 0.

a) \(\left(x+5\right).6-7=29\)

\(\Rightarrow\left(x+5\right).6=29+7\)

\(\Rightarrow\left(x+5\right).6=36\)

\(\Rightarrow\left(x+5\right)=36:6=6\)

\(\Rightarrow x=6-5=1\)

b) \(5x-3x=12-3.2\)

\(\Rightarrow2x=6\Rightarrow x=6:2=3\)

c) \(\dfrac{1}{4}.3< x< \dfrac{51}{50}.4\)

\(\Rightarrow\dfrac{3}{4}< x< \dfrac{102}{25}\)

Ta có: f(x) + h(x) = g(x)

Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)

            = x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1

            = ( x4 – x4) – x3 + (x2 + 3x2 ) – x + (5+ 1)

            = -x3 + 4x2 – x + 6

Ta có: f(x) – h(x) = g(x)

Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)

            = x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5

            = (x4 – x4) + x3 – (3x2 + x2) + x - (1+ 5)

            = x3 – 4x2 + x – 6