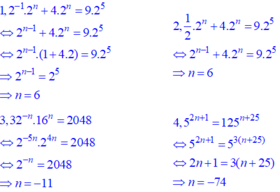Số nguyên n thỏa mãn \(\frac{1}{2}\).2n+4.2n=9.25 là n=.......
NP
Những câu hỏi liên quan
Tìm số nguyên n, biết
1
)
2
−
1
.2
n
+
4.2
n
9.2
5
2
)
1
2
.2
n
+
4.2
n
9.2
5
3...
Đọc tiếp
Tìm số nguyên n, biết
1 ) 2 − 1 .2 n + 4.2 n = 9.2 5
2 ) 1 2 .2 n + 4.2 n = 9.2 5
3 ) 32 − n .16 n = 2048
4 ) 5 2 n + 1 = 125 n + 25
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ gt \(\Rightarrow n,k\ge2\)
Ta có:
\(\left\{{}\begin{matrix}n^3-n-1>1;n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}n^3-n-1=p^r\\n^2+n-1=p^s\end{matrix}\right.\) trong đó \(\left\{{}\begin{matrix}r\ge s>0\\r+s=k\end{matrix}\right.\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác:
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\left\{{}\begin{matrix}p=5\\k=2\end{matrix}\right.\)
Vậy bộ số (n,k,p)=(2,2,5)
Đúng 2
Bình luận (0)
\(...\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\).
Do đó \(\left\{{}\begin{matrix}n^2+n-1=p^v\\n^3-n-1=p^u\end{matrix}\right.\left(v,u\in N;v+u=k\right)\).
+) Với n = 2 ta có \(p^k=25=5^2\Leftrightarrow p=5;k=2\)
+) Với n > 2 ta có \(n^3-n-1>n^2+n-1\Rightarrow v>u\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow\left(n^2+n-1\right)\left(n-1\right)+n-2⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\)
\(\Rightarrow\left(n-2\right)\left(n+3\right)⋮n^2+n-1\)
\(\Rightarrow6⋮n^2+n-1\).
Không tồn tại n > 2 thoả mãn
Vậy...
Đúng 2
Bình luận (0)
CÓ BAO NHIÊU SỐ NGUYÊN n THỎA MÃN n^2+2n-6/n-2 LÀ SỐ NGUYÊN
Ta có:
\(\frac{n^2+2n-6}{n-2}=\frac{\left(n^2-2n\right)+\left(4n-8\right)+2}{n-2}=\frac{n\left(n-2\right)+4\left(n-2\right)+2}{n-2}\)
\(=\frac{\left(n+4\right)\left(n-2\right)+2}{n-2}=n+4+\frac{2}{n-2}\)
để phân thức trên là số nguyên<=>2 chia hết cho n-2
hay n-2 thuộc Ư(2)
=>n-2=(-2;-1;1;2)
<=>n=(0;1;3;4)
Đúng 0
Bình luận (0)
Bài 4:
a) Tìm số nguyên thỏa mãn -2n+1 chia hết cho n-2
b) tìm số nguyên n thỏa mãn (n-2) chia hết cho (3n+1)
không ạ mình hỏi các bạn bài này ạ!
Tìm số nguyên dương n nhỏ nhất lớn hơn 1 thỏa mãn \(A=\frac{\left(n+1\right)\left(2n+1\right)}{6}\) là 1 số chính phương
TH1) Với n = 6k
ta có: \(\left(n+1\right)\left(2n+1\right)=\left(6k+1\right)\left(12k+1\right)\) không chia hết cho 6
=> Loại
TH2) Với n = 6k+1
ta có: \(\left(n+1\right)\left(2n+1\right)=\left(6k+2\right)\left(12k+3\right)⋮6\)
=> \(A=\frac{\left(6k+2\right)\left(12k+3\right)}{6}=\left(3k+1\right)\left(4k+1\right)\)là số chính phương
Lại có: ( 3k + 1 ; 4k + 1 ) = ( 3k + 1 ; k ) = ( 2k + 1 ; k ) = ( k + 1 ; k ) = ( k ; 1 ) = 1
=> 3k + 1 và 4k + 1 đồng thời là 2 số chính phương
+) Với k \(\equiv\)\(1,3,5,7\)(mod 8 ) => 4k + 1 không là số cp
+) Với k \(\equiv\)2; 4; 6 ( mod 8) => 3k + 1 không là số chính phương
=> k \(\equiv\)0 ( mod 8) => k = 8h
=> Tìm h bé nhất để 24h + 1 và 32h + 1 là số chính phương(1)
+) Với h \(\equiv\)\(3,4,6\)( mod7) => 24k + 1 không là số chính phương
+) Với h \(\equiv\)1 (mod 7 ) => 32h + 1 không là số cp
=> h \(\equiv\)0; 2; 5 (mod 7 )
=> h = 7m hoặc h = 7n + 2 hoặc h = 7t + 7 ( với m;n; t nguyên dương )
Nếu m = 1 => h = 7 => 24h + 1 = 169 và 32h + 1 = 225 là hai số chính phương và h nhỏ nhất
=> n = 6k + 1 và k = 8h = 56
=> n = 337
=> A = 38025 là số chính phương
TH3) Với n = 6k + 2
ta có: \(\left(n+1\right)\left(2n+1\right)=\left(6k+3\right)\left(12k+5\right)\)không chia hết cho 6
TH4) Với n = 6k + 3
ta có: \(\left(n+1\right)\left(2n+1\right)=\left(6k+4\right)\left(12k+7\right)\)không chia hết cho 6
TH5) Với n = 6k + 4
ta có: \(\left(n+1\right)\left(2n+1\right)=\left(6k+5\right)\left(12k+9\right)\)không chia hết cho 6
TH6) Với n = 6k + 5
ta có \(\left(n+1\right)\left(2n+1\right)=\left(6k+6\right)\left(12k+11\right)⋮6\)
=> \(A=\frac{\left(6k+6\right)\left(12k+11\right)}{6}=\left(k+1\right)\left(12k+11\right)\)
mà ( k + 1; 12k + 11 ) = 1
=> k + 1 và 12k + 11 là 2 số chính phương
tuy nhiên 12k + 11 chia 12 dư 11 mà 1 số chính phương chia 12 không dư 11
=> Trường hợp này loại
Vậy n = 337
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ giả thiết \(\Rightarrow n,k\ge2\)
Ta có:
\(\hept{\begin{cases}n^3-n-1>1,n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n^3-n-1=p^r\\n^2+n-1=p^s\end{cases}}\) trong đó \(\hept{\begin{cases}r\ge s\ge0\\r+s=k\end{cases}}\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác :
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\hept{\begin{cases}p=5\\k=2\end{cases}}\)
Vậy bộ số cần tìm là (n,k,p)=(2,2,5)
Cho n là một số nguyên dương thỏa mãn n+1 và 2n+1 đồng thời là 2 số chính phương(số chính phương là bình phương của 1 số nguyên ) CMR: n chia hết 24
Bài này hay thật mình thì chỉ nghĩ ra mỗi cách này. Nhưng ko biết vs học phô thông thì tư duy thế nào
1 số chính phương có tận cùng bằng 0,1,4,5,6,9
N+1 tận cùng =9=> n tận cùng bằng 8 => 2n+1 tận cùng =7 => loại
(2n+1)-(n+1)=n=a^2-b^2=(a-b)(a+b)
2n+1 là số lẻ => a lẻ
N chẵn=> b chẵn
1 số chính phương chia cho 4 dư 0 hoặc 1 => (a+b)(a-b) chia hết cho 8
Còn nó chia hết cho 3 hay không thì phải dùng định lý của fermat đẻ giải
http://en.wikipedia.org/wiki/Fermat%27s_little_theorem
như vậy chưng minh no chia het cho 8 và 3 là có thể két luạn nó chia hêt cho 24
Đúng 0
Bình luận (0)
ùi hơi khó thế này thì có làm đc ko
Tìm tất cả các số nguyên dương thỏa mãn 2n2+3n+1 là số chính phương và n+5 là số nguyên tố
Tìm số nguyên n thỏa mãn 2n+1 chia hết cho n-2
2n+1:n-2
suy ra n+n-2+3:n-2
n+3:n-2
n-2+5:n-2
5:n-2
":" là dấu chia hết nha :3 típ nè
suy ra n-2 thuộc Ư(5)= (ngoặc vuông) 1;5 (ngoặc vuông)
TH1: n-2 =1
n=2+1
n=3
TH2: n-2=5
n=5+2
n=7
suy ra n thuộc (ngoặc vuông) 2,7 (ngoặc vuông)
Xong rùi nè
nhớ chọn câu trả lời của mk nha :Đ TYM TYM =))
Đảm bảo đúng 100% (9,3 đ giữa kì ó)
\(\left(2n+1\right)⋮\left(n-2\right)\Leftrightarrow\left[2\left(n-2\right)+5\right]⋮\left(n-2\right)\Leftrightarrow5⋮\left(n-2\right)\)
\(\Leftrightarrow n-2\inƯ\left(5\right)=\left\{-5,-1,1,5\right\}\Leftrightarrow n\in\left\{-3,1,3,7\right\}\).
tìm số nguyên n thỏa mãn 2n + 1 chia hết cho n-2
Ta có \(\hept{\begin{cases}2n+1⋮n-2\\n-2⋮n-2\end{cases}\Rightarrow\hept{\begin{cases}2n+1⋮n-2\\2n-4⋮n-2\end{cases}}}\)
\(\Rightarrow2n+1-2n+4⋮n-2\)
\(\Rightarrow5⋮n-2\)
\(\Rightarrow n-2\in\left\{1;5\right\}\)
\(\Rightarrow n\in\left\{3;7\right\}\)
Đúng 0
Bình luận (0)
Ta có: 2n+1\(⋮\)n-2
\(\Rightarrow\)2n-4+5\(⋮\)n-2
\(\Rightarrow\)2(n-2)+5\(⋮\)n-2
Mà 2(n-2)\(⋮\)n-2 (\(\forall\)n\(\in\)Z)
Nên 5\(⋮\)n-2
n-2\(\in\)Ư(5)=\([\)-1;1;5;-5\(]\)(dấu ngoặc sai nhé)
n\(\in\)\([\)1;3;7;-3\(]\)
Đúng 0
Bình luận (0)
\(2n+1⋮n-2\)
\(\Rightarrow2\left(n-2\right)+5⋮n-2\)
\(\Rightarrow5⋮n-2\)
\(\Rightarrow n-2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
\(\Rightarrow n\in\left\{3;1;7;-3\right\}\)
Vậy.............................
Đúng 0
Bình luận (0)