Số mặt phẳng đối xứng của hình hộp đứng có đáy là hình vuông là:
A. 3.
B. 4.
C. 6.
D. 5.
Một hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. 1
B. 3
C. 4
D. 2
Chọn B.
Phương pháp:
Sử dụng lý thuyết khối đa diện để là bài toán.
Cách giải:
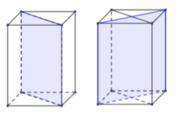
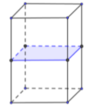
Hình đã cho có 3 mặt phẳng đối xứng.
Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
A. 3
B. 1
C. 5
D. 4
Đáp án C
4 mặt phẳng cắt theo chiều dọc và 1 mặt phẳng cắt theo chiều ngang.
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng ?
A. 1
B. 2
C. 3
D. 4
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 1
B. 2
C. 3
D. 4
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 3.
B. 2.
C. 4.
D. 1
Chọn đáp án A.
Hình hộp đứng có đáy là hình thoi có 3 mặt phẳng đối xứng như hình vẽ dưới
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng
A. 1
B. 3
C. 4
D. 2
Hình hộp đứng có đáy hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. Bốn.
B. Năm.
C. Sáu.
D. Ba.
Hình hộp đứng có đáy là hình thoi có 3 mặt phẳng đối xứng, gồm 2 mặt chéo và 1 mặt phẳng đi qua trung điểm cạnh bên và song song với 2 mặt đáy.
Chọn đáp án D.
Hình hộp chữ nhật chỉ có hai đáy là hai hình vuông có tất cả bao nhiêu mặt phẳng đối xứng?
A. 4
B. 3
C. 9
D. 5
Đáp án D
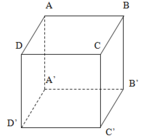
Gọi hình hộp đó là ABCDA’B’C’D’
Gọi M,N,P,Q là trung điểm của AB,BC,CD,AD
M’,N’,P’,Q’ là trung điểm của A’B’,B’C’,C’D’,A’D’
E,F,G,H là trung điểm của AA’,BB’,CC’,DD’
Các mặt phẳng đối xứng của hình hộp là :
(MPP’M’),(NQQ’N’),(ACC’A’),(BDD’B’),(EFGH)
Hình hộp chữ nhật chỉ có hai đáy là hai hình vuông có tất cả bao nhiêu mặt phẳng đối xứng?
A. 4
B. 3
C. 9
D. 5
Đáp án D

Gọi hình hộp đó là ABCDA’B’C’D’
Gọi M,N,P,Q là trung điểm của AB,BC,CD,AD
M’,N’,P’,Q’ là trung điểm của A’B’,B’C’,C’D’,A’D’
E,F,G,H là trung điểm của AA’,BB’,CC’,DD’
Các mặt phẳng đối xứng của hình hộp là :
(MPP’M’), (NQQ’N’), (ACC’A’), (BDD’B’), (EFGH)