Tìm hai số phức, biết tổng của chúng bằng tích của chúng và bằng 2
A. z 1 = - 1 + i ; z 2 = - 1 - i
B. z 1 = 1 + i ; z 2 = - 1 - i
C. z 1 = - 1 + i ; z 2 = 1 - i
D. z 1 = 1 + i ; z 2 = 1 - i
PB
Những câu hỏi liên quan
Tìm hai số phức biết rằng tổng của chúng bằng 4-i và tích của chúng bằng 5(1-i) A.
z
1
3
+
2
i
;
z
2
1
-
i
B.
z
1
3
+
i
;
z
2
1
-
2...
Đọc tiếp
Tìm hai số phức biết rằng tổng của chúng bằng 4-i và tích của chúng bằng 5(1-i)
A. z 1 = 3 + 2 i ; z 2 = 1 - i
B. z 1 = 3 + i ; z 2 = 1 - 2 i
C. z 1 = 3 - i ; z 2 = 1 + 2 i
D. z 1 = 3 + i ; z 2 = 1 + 2 i
Tìm hai số phức biết rằng tổng của chúng bằng 4-i và tích của chúng bằng
5
(
1
-
i
)
Đọc tiếp
Tìm hai số phức biết rằng tổng của chúng bằng 4-i và tích của chúng bằng 5 ( 1 - i )
Tìm hai số phức, biết tổng của chúng bằng tích của chúng và bằng 2.
Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4.
Hai số phức có tổng bằng 3, tích bằng 4 là nghiệm của phương trình:
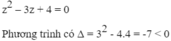
⇒ Phương trình có hai nghiệm: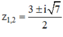 
Vậy hai số cần tìm là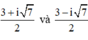 
Đúng 0
Bình luận (0)
Tìm hai số phức, biết tổng của chúng bằng 3 và tích của chúng bằng 4 ?
Giả sử hai số cần tìm là z1 và z2.
Ta có: z1 + z2 = 3; z1. z2 = 4
Rõ ràng, z1, z2 là các nghiệm của phương trình:
(z – z1)(z – z2) = 0 hay z2 – (z1 + z2)z + z1. z2 = 0
Vậy z1, z2 là các nghiệm của phương trình: z2 – 3z + 4 = 0
Phương trình có Δ = 9 – 16 = -7
Vậy hai số phức cần tìm là: z1=3+i√72,z2=3−i√72
Đúng 0
Bình luận (0)
Bài 1 : Tìm hai số biết tổng gấp 3 lần hiệu và bằng nửa tích của chúng .
Bài 2 : Tìm hai số biết tổng gấp 5 lần hiệu và bằng 1/6 tích của chúng .
Bài 1: Tổng trừ hiệu chính bằng hai lần số bé, từ đề bài ta suy ra 2 lần hiệu bằng hai lần số bé. Nói cách khác hiệu bằng số bé hay số lớn gấp đối số bé.
Tích của số bé và số lớn chính là tích số bé và hai lần số bé chia 2 hay chính bằng số bé nhân số bé. Tổng bằng 3 lần số bé và bằng số bé nhân số bé nên số bé bằng 3 và số lớn bằng 6.
Bài 2: Tương tự. Ta tìm được số bé là 10, số lớn là 15.
Đúng 0
Bình luận (0)
Cho hai số phức z và w biết chúng thỏa mãn hai điều kiện
(
1
+
i
)
z
1
-
i
+
2
2
,w iz Giá trị lớn nhất của M |w - z| bằng A. 4 B.
2
2...
Đọc tiếp
Cho hai số phức z và w biết chúng thỏa mãn hai điều kiện ( 1 + i ) z 1 - i + 2 = 2 ,w = iz Giá trị lớn nhất của M = |w - z| bằng
A. 4
B. 2 2
C. 4 2
D. 2
1.Tìm hai số tự nhiên a và b (a > b) có tổng bằng 224,biết rằng ƯCLN của chúng bằng 28
2.tìm hai số tự nhiên a và b(a>b) có tích bằng 1944,biết rằng ƯCLN của chúng bằng 18
tìm hai số biết tổng của chúng gấp 3 lần hiệu và bằng 1/2 tích của chúng.