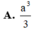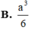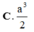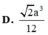Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Thể tích khối tứ diện A B ' C ' D ' bằng
A. a 3 3
B. a 3 6
C. a 3 2
D. 3 a 3 12
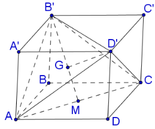
Cho ABCD.A′B′C′D′ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD′B′ là
A. 8 a 3 3
B. 4 a 3 3
C. 2 a 3 3
D. 8 a 3 9
Đáp án C
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có

Cho hình lập phương ABCD.A′B′C′D′ABCD.A′B′C′D′ cạnh aa và một điểm MM trên cạnh AB,AM=x,0<x<aAB,AM=x,0<x<a. Xét mặt phẳng (PP) đi qua điểm MM và chưa đường chéo A′C′A′C′ của hình vuông A′B′C′D′.A′B′C′D′.
1.1. Tính diện tích của thiết diện của hình lập phương cắt bởi mặt phẳng (PP).
2.2. Mặt phẳng (PP) chia hình lập phương thành hai khối đã diện. Hãy tìm xx để thể tích của một trong hai khối đa diện đó gấp đôi thể tích của khối đa diện kia.
1Tính thể tích của hình lập phương có cạnh là 12,6 cm ?
A. 2100,376cm32100,376cm3
B. 2000,376cm32000,376cm3
C. 2300,376cm32300,376cm3
D. 2200,376cm32200,376cm3
2Tính thể tích của hình lập phương có cạnh là 2,1 cm ?
A. 9,261cm39,261cm3
B. 11,261cm311,261cm3
C. 12,261cm312,261cm3
D. 10,261cm310,261cm3
3Tính thể tích của hình lập phương có cạnh là 14 m ?
A. 1744m31744m3
B. 4744m34744m3
C. 2744m32744m3
D. 3744m33744m3
4Một hình lập phương có cạnh 7 cm. Nếu cạnh của hình lập phương tăng lên 4 lần thì thể tích hình lập phương tăng lên mấy lần?
A. 36 lần
B. 64 lần
C. 16 lần
D. 54 lần
5Mickey có một khối rubik hình lập phương có thể tích là 64 xăng-ti-mét khối, Donald có một khối rubik hình lập phương có thể tích là 216 xăng-ti-mét khối. Hỏi cạnh khối rubik của Donald dài hơn cạnh khối rubik của Mickey bao nhiêu xăng-ti-mét ?
A. 3 cm
B. 1 cm
C. 4 cm
D. 2 cm
Câu 1 :Diện tích của một hình tròn có bán kính 2/5 m là : ... m
Câu 2 :Thể tích hình lập phương A gấp 8 lần thể tích hình lập phương B . Vậy cạnh của hình lập phương A gấp cạnh của hình lập phương B số lần là :
A.2 lần B.4 lần C.6 lần D.8 lần
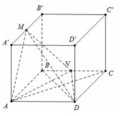
Cho hình lập phương ![]() có cạnh a. Gọi M là trung điểm A', B', N' là trung điểm Tính thể tích của khối tứ diện ADMN
có cạnh a. Gọi M là trung điểm A', B', N' là trung điểm Tính thể tích của khối tứ diện ADMN
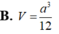
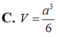
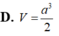
Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng 2 k 3 12 . Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a 2 . Tính theo a thể tích khối tứ diện A C B ' D ' .
A. 2 2 a 3 3
B. 2 a 3 6
C. 2 a 3 2
D. a 3 3
Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:
1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng
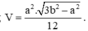
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là ![]()
3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là
![]()
4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là
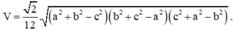
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a 3
C. a 3 12
D. a 3 24
Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
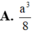
![]()
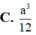
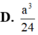
Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Mặt phẳng (MB'D'N) chia khối lập phương đã cho thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A. Thể tích của khối đa diện (H) bằng:
A. a 3 9 B. a 3 6
C. a 3 4 D. 7 a 3 24
Chọn D.
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Thể tích khối tứ diện AB’C’D’ bằng