Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng ?
A. Hàm số nghịch biến trên i
B. Hàm số đồng biến trên mỗi khoảng - ∞ ; - 1 v à - 1 ; + ∞
C. Hàm số luôn đồng biến trên i
D. Hàm số luôn nghịch biến trên i\{-1}
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Kết luận nào sau đây về tính đơn điệu của hàm số y = x + 3 x - 3 là đúng?
A. Hàm số đồng biến trên các khoảng (-∞; 3) và (3; +∞)
B. Hàm số luôn đồng biến trên R\{3}
C. Hàm số nghịch biến trên các khoảng (-∞; 3) và (3; +∞)
D. Hàm số luôn nghịch biến trên R\{3}
Tập xác định: D = R\{3}
Đạo hàm 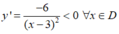
Do đó, hàm số nghịch biến trên các khoảng (-∞; 3) và (3; +∞)
Chọn C.
Cho hàm số y=f(x) xác định và liên tục trên R. Đồ thị của hàm số y=f'(x) hình trên. Kết luận nào sau đây về tính đơn điệu của hàm số y = f x − 2 x + 2018 là đúng?

A. Hàm số đồng biến trên R
B. Hàm số đồng biến trên các khoảng − ∞ ; 0
C. Hàm số đồng biến trên khoảng 1 ; + ∞
D. Hàm số nghịch biến trên khoảng − 1 ; 5
Đáp án C
Ta có y ' = f ' x − 2 dựa trên đồ thị ta thấy x ∈ 1 ; + ∞ ⇒ f ' x > 2 ⇒ f ' x − 2 > 0 ⇒ y đồng biến
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số luôn đồng biến trên ℝ \ − 1
B. Hàm số đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
C. Hàm số luôn nghịch biến trên ℝ \ − 1
D. Hàm số nghịch biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
Đáp án B
Ta có y ' = 1 x + 1 2 > 0 , ∀ x ≠ − 1 ⇒ hàm số đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số đồng biến trên các khoảng ( - ∞ ; - 1 ) và ( - 1 ; + ∞ )
B. Hàm số luôn luôn đồng biến trên R \ {-1}
C. Hàm số nghịch biến trên các khoảng ( - ∞ ; - 1 ) và ( - 1 ; + ∞ )
D. Hàm số luôn luôn nghịch biến trên R \ {-1}
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số đồng biến trên R \ - 1
B. Hàm số nghịch biến trên khoảng - ∞ ; - 1 và - 1 ; + ∞
C. Hàm số đồng biến trên khoảng - ∞ ; - 1 và - 1 ; + ∞
D. Hàm số đồng biến trên khoảng - ∞ ; - 1 ∪ - 1 ; + ∞
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số đồng biến trên các khoảng (-∞;-1) và (-1;+∞)
B. Hàm số luôn luôn đồng biến trên R/{-1}
C. Hàm số nghịch biến trên các khoảng (-∞;-1) và (-1;+∞)
D. Hàm số luôn luôn nghịch biến trên R/{-1}
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x - 1 là đúng?
A. Hàm số luôn nghịch biến trên ℝ \ 1
B. Hàm số luôn đồng biến trên - ∞ ; 1 và 1 ; + ∞ .
C. Hàm số luôn nghịch bến trên - ∞ ; 1 và 1 ; + ∞ .
D. Hàm số luôn đồng biến trên ℝ \ 1
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số luôn luôn nghịch biến trên ℝ \ − 1 .
B. Hàm số nghịch biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
C. Hàm số đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
D. Hàm số luôn luôn đồng biến trên ℝ \ − 1 .
Đáp án C
TXĐ: D = ℝ \ − 1 ta có: y ' = 1 x + 1 2 > 0 ∀ x ∈ D
Do đó hàm số đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞
Kết luận nào sau đây về tính đơn điệu của hàm số y = 2 x + 1 x + 1 là đúng?
A. Hàm số đồng biến trên các khoảng (-∞; -1) và (-1; +∞)
B. Hàm số luôn luôn đồng biến trên R \ {-1}
C. Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞)
D. Hàm số luôn luôn nghịch biến trên R \ {-1}
Đáp án A.
Tập xác định D = R \ {-1}.
Ta có ![]()
Suy ra hàm số đã cho đồng biến trên từng khoảng xác định của nó.