Rút gọn biểu thức sau A=(3/1.2)^2+(5/2.3)^2+(7/3.4)^2+...+(2n+1/n^2+1)^2
GH
Những câu hỏi liên quan
Rút gọn \(A=\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
Ta có:
\(A=\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(=\frac{3}{1^2.2^2}+\frac{5}{2^2.3^2}+\frac{7}{3^2.4^2}+...+\frac{2n+1}{n^2\left(n+1\right)^2}\)
\(=\frac{3}{1.4}+\frac{5}{4.9}+\frac{7}{9.16}+...+\frac{2n+1}{n^2\left(n+1\right)^2}\)
\(=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{9}+...+\frac{2n+1}{n^2}-\frac{2n+1}{\left(n+1\right)^2}\)
\(=1-\frac{2n+1}{\left(n+1\right)^2}\)
Vậy \(A=\frac{2n+1}{\left(n+1\right)^2}\)
Đúng 0
Bình luận (0)
a) Phân tích đa thức thành nhân tử: x(x+2)(x2+2x+2)+1
b) Rút gọn biểu thức: A = \(\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{2n+1}{[n\left(n+1\right)]^2}\)![]()
Bạn thử giải câu này xem
NHỚ ĐỌC KỸ ĐỀ ĐẤY
https://olm.vn/hoi-dap/detail/211451950700.html?pos=476647086293
Đúng 0
Bình luận (0)
\(x\left(x+2\right)\left(x^2+2x+2\right)+1\)
\(=\left(x^2+2x\right)\left(x^2+2x+2\right)+1\)
Đặt: \(x^2+2x=t\)
khi đó: \(\left(x^2+2x\right)\left(x^2+2x+2\right)+1=t\left(t+2\right)+1=\left(t+1\right)^2\)
\(=\left(x^2+2x+1\right)^2=\left(x+1\right)^4\)
b) Xét: \(\left(n+1\right)^2-n^2=\left(n+1+n\right)\left(n+1-n\right)=2n+1\)
Khi đó:
\(A=\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(A=\frac{2^2-1^2}{1^2.2^2}+\frac{3^2-2^2}{2^2.3^2}+\frac{4^2-3^2}{3^2.4^2}+...+\frac{\left(n+1\right)^2-n^2}{n^2.\left(n+1\right)^2}\)
\(A=1-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}+...+\frac{1}{n^2}-\frac{1}{\left(n+1\right)^2}\)
\(A=1-\frac{1}{\left(n+1\right)^2}\)
Đúng 0
Bình luận (0)
rút gọn phân thức:\(A=\dfrac{3}{\left(1.2\right)^2}+\dfrac{5}{\left(2.3\right)^2}+\dfrac{7}{\left(3.4\right)^2}+...+\dfrac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(A=\dfrac{3}{\left(1\cdot2\right)^2}+\dfrac{5}{\left(2\cdot3\right)^2}+\dfrac{7}{\left(3\cdot4\right)^2}+...+\dfrac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(A=\dfrac{3}{1\cdot4}+\dfrac{5}{4\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{2n+1}{n^2\cdot\left(n^2+2n+1\right)}\)
\(A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{n^2}-\dfrac{1}{n^2+2n+1}\)
\(A=1-\dfrac{1}{n^2+2n+1}\)
\(A=\dfrac{n\left(n+2\right)}{\left(n+1\right)^2}\)
Đúng 0
Bình luận (0)
rút gọn biểu thức
1^2/1.2*2^2/2.3*3^2/3.4*...*19^2/19.20
giúp mình với nha cảm ơn
Hãy rút gọn biểu thức M=(12/1.2).(22/2.3).(32/3.4).....=102/10.11
Câu hỏi của pham nhu nguyen - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Rút gọn biểu thức
A
3
1
.
2
+
5
(
2
.
3
)
2
+
.
.
.
+
2
n
+
1
[
n
(
n
+
1
)...
Đọc tiếp
Rút gọn biểu thức A = 3 1 . 2 + 5 ( 2 . 3 ) 2 + . . . + 2 n + 1 [ n ( n + 1 ) ] 2
Xét biểu thức tổng quát: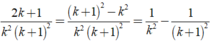
Khi đó ta có: 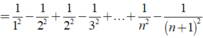
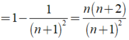
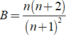
Vậy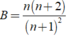
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau A =
3/1^2.2^2+5/2^2.3^2+7/3^2.4^2+...+(n+1)^2-1^2/n^2(n+1)^2
ruts gọn biểu thức: 3/(1.2)2 + 5/(2.3)2 + 7/(3.4)2 + ...+ 2n+1/(n(n+1))2
\(\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+...+\frac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(=\frac{2^2-1^2}{\left(1.2\right)^2}+\frac{3^2-2^2}{\left(2.3\right)^2}+...+\frac{\left(n+1\right)^2-n^2}{\left[n\left(n+1\right)\right]^2}\)
\(=1-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+...+\frac{1}{n^2}-\frac{1}{\left(n+1\right)^1}\)
\(=1-\frac{1}{n^2+2n+1}\)
\(=\frac{n^2+2n}{n^2+2n+1}\)
Đúng 0
Bình luận (0)
\(\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(=1-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}+...+\frac{1}{n^2}-\frac{1}{\left(n+1\right)^2}\)
\(=1-\frac{1}{\left(n-1\right)^2}\)
\(=\frac{\left(n-1\right)^2-1}{\left(n-1\right)^2}\)
Đúng 0
Bình luận (0)
Rút gọn: \(A=\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+....+\frac{2n+1}{\left(n.\left(n+1\right)\right)^2}\)
Cho a1, a2, a3,........., a2016 là các STN và tổng chúng chia hết cho 3. CMR: A=a13+a23+..............+a20163 chia hết cho 3.


