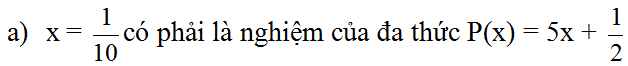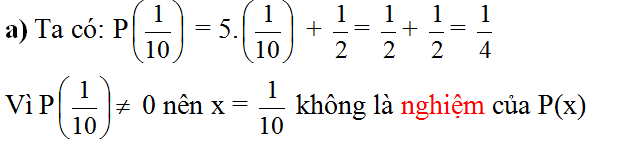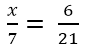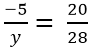Bài 2 (trang 48 SGK Toán 3)
PB
Những câu hỏi liên quan
Kiểm tra xem:
b) Mỗi số x = 1; x = 3 có phải là một nghiệm của đa thức Q(x) = x2 – 4x + 3 không.
b) Ta có: Q(1) = 12 – 4.1 + 3 = 1 – 4 + 3 = 0
=> x = 1 là nghiệm của Q(x)
Q(3) = 32 – 4.3 + 3 = 9 – 12 + 3 = 0
=> x = 3 là nghiệm của Q(x)
Đúng 0
Bình luận (0)
Giups mình làm bài 48 trang 121 sgk toán 6 với
cho mình hỏi có phải sách vnen không vậy?
Đúng 0
Bình luận (0)
Theo đề bài sau bốn lần căng dây đo liên tiếp thì khoảng cách giữa hai đầu dây và mép tường còn lại bằng 1515 độ dài sợi dây, nên chiều rộng lớp học sẽ là độ dài của bốn lần sợi dây và 1515 độ dài sợ dây đó.
(chiều rộng lớp học) = (độ dài sau 4 lần đo) + (1/5 độ dài sợi dây)
Chiều dài của 1/5 sợi dây là: 1,25 . 1/5 = 0,25 m
Chiều rộng lớp học là: 4.1,25 + 0,25 = 5,25 m
Vậy chiều rộng lớp học là 5,25 m.
Đúng 0
Bình luận (0)
Ai biết làm mấy bài từ 106 -> 114 sgk trang 48 -> 50 không???? Toán lớp 6 tập 2
mik mới làm trang 43 chưa hox trang 50
Đúng 0
Bình luận (0)
Mấy bài đó quá dễ nhưng wa dài,ko tiện trình bày!
Đúng 0
Bình luận (0)
bài 48 trang 93 sgk toán 8 tập 1 làm thế nào zây? giúp mình vs
.
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = AC.
HG là đường trung bình của ∆ACD nên HG = AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)
Đúng 0
Bình luận (0)
Thuật toán tính tiền trong ví dụ 2, ví dụ 3 trang 48 SGK, vẽ sơ đồ hoạt động cho điều kiện của thuật toán

Bài 9 (trang 48 SGK Toán 9 Tập 1)
Cho hàm số bậc nhất $y=(m-2) x+3$. Tìm các giá trị của $m$ để hàm số :
a) Đồng biến ;
b) Nghịch biến.
a, hàm số bậc nhất y = (m-2)x +3 đồng biến <=> m-2 > 0
<=> m >2
b,hàm số bậc nhất y =(m-2)x +3 nghịch biến <=> m - 2 <0
<=> m < 2
a, Để hàm số trên đồng biến khi
\(m-2>0\Leftrightarrow m>2\)
b, Để hàm số trên nghịch biến khi
\(m-2< 0\Leftrightarrow m< 2\)
a) để pt đồng biến thì m-2>0\(\Leftrightarrow\)m>2
b) để pt nghịch biến thì m-2<0\(\Leftrightarrow\)m<-2
Xem thêm câu trả lời
Bài 48 (trang 29 SGK Toán 9 Tập 1)
Khử mẫu của biểu thức lấy căn
$\sqrt{\dfrac{1}{600}}; \sqrt{\dfrac{11}{540}}$ ; $\sqrt{\dfrac{3}{50}} ; \sqrt{\dfrac{5}{98}}$ ; $\sqrt{\dfrac{(1-\sqrt{3})^{2}}{27}}$
\(\sqrt{\dfrac{1}{600}}\)=\(\sqrt{\dfrac{1}{10^2\cdot6}}\)=\(\sqrt{\dfrac{1\cdot6}{10^2\cdot6\cdot6}}\)=\(\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}\)=\(\sqrt{\dfrac{11\cdot540}{540\cdot540}}\)=\(\dfrac{\sqrt{5940}}{540}\)=\(\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}\)=\(\sqrt{\dfrac{3\cdot50}{50\cdot50}}\)=\(\dfrac{\sqrt{150}}{50}\)=\(\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}\)=\(\sqrt{\dfrac{5\cdot98}{98\cdot98}}=\dfrac{\sqrt{490}}{98}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)
\(\sqrt{\dfrac{1}{600}}=\dfrac{\sqrt{6}}{60}\)
\(\sqrt{\dfrac{11}{540}}=\dfrac{\sqrt{165}}{90}\)
\(\sqrt{\dfrac{3}{50}}=\dfrac{\sqrt{6}}{10}\)
\(\sqrt{\dfrac{5}{98}}=\dfrac{\sqrt{10}}{14}\)
\(\sqrt{\dfrac{\left(1-\sqrt{3}\right)^2}{27}}=\dfrac{3-\sqrt{3}}{9}\)
Xem thêm câu trả lời
giải theo đúng 1 bài tìm x cho mik nha
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
Đúng 3
Bình luận (0)
a) x/7=6/21
x.21=6.7
x.21=42
x=42:21
x=2
b) -5/y=20/28
y.20=(-5).28
y.20= -140
y= (-140):20
y= -7
TICK CHO MÌNH NHA^^
Đúng 1
Bình luận (0)
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 3 (trang 177 SGK Toán 4):