abcdeg chia hết cho 23 và 9
giúp mình nha !
7)Chứng minh rằng :
a) abcabc chia hết cho 7,11,13
b) abcdeg chia hết cho 23 và 29 , biết rằng abc=2.deg
8)Chứng minh rằng nếu ab+cd+eg chia hết cho 11 thì abcdeg chia hết cho 11
7)a) abcabc : abc = 1001
abcabc = 1001 x abc . Mà 1001 chia hết cho 7; 11; 13 nên 1001 x abc chia hết cho 7; 11; 13 . Vậy abcabc chia hết cho 7; 11; 13 ( đpcm)
b .Vì abc = 2 . deg nên abcdeg : deg = 2001
abcdeg = 2001 x deg. Do 2001 chia hết cho 23 và 29 nên 2001 x deg chia hết cho 23 và 29 . Vậy abcdeg chia hết cho 23 và 29 ( đpcm)
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
1028+8/chứng tỏ chia hết cho 9
giúp mình với
TL:
Ta có: \(10^{28}+8=100...00\)(\(28\) chữ số \(0\)) \(+8⋮9\) ( Vì \(1+8=9⋮9\))
Vậy\(10^{28}+8⋮9\) thoả mãn bài toán
CHÚC BẠN HỌC TỐT NHÉ.
1028 + 8 chia hết cho 9
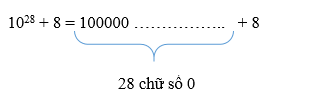
1028 + 8 = 1 + 0 + 0 + ............... + 8 = 9
Mà \(9⋮9\)
\(\Rightarrow10^{28}+8⋮9\)
C m rằng abcdeg chia hết cho 23 và 29 biết abc 2deg.
Chứng minh rằng abcdeg chia hết cho 23 và 29, biết rằng abc = 2.deg
Ta có: \(\overline{abcdeg}=1000\overline{abc}+\overline{deg}=2000\overline{deg}+\overline{deg}=2001\overline{deg}\)
Vì 2001 chia hết cho 23 và 29 \(\Rightarrow2001\overline{deg}\) chia hết cho 23 và 29
Vậy \(\overline{abcdeg}\) chia hết cho 23 và 29
\(\overline{abcdeg}=1000.\overline{abc}+\overline{deg}\\ =1000.2.\overline{deg}+\overline{deg}\\ =\left(2000+1\right)\overline{deg}\\ =2001.\overline{deg}\\ =23.29.3.\overline{deg}⋮23,29\left(đcpcm\right)\)
Chứng minh rằng abcdeg chia hết cho 23 và 29. Biết rằng abc= 2x deg
\(\overline{abcdeg}\)
= \(\overline{abc}\) x 1000 + \(\overline{deg}\)
= \(\overline{deg}\) x 2 x 1000 + \(\overline{deg}\) x 1
= \(\overline{deg}\) x 2000 + \(\overline{deg}\) x 1
= \(\overline{deg}\) x (2000 + 1)
= \(\overline{deg}\) x 2001
= \(\overline{deg}\) x 23 x 29 x 3 ⋮ 23; và 29 (đpcm)
Chứng minh rằng abcdeg chia hết cho 23 và 29. Biết rằng abc= 2x deg
\(\overline{abcdeg}=1000.\overline{abc}+\overline{deg}=1000.2.\overline{deg}+\overline{deg}=\)
\(=2001.\overline{deg}=23.87.\overline{deg}=29.69.\overline{deg}\)
\(\Rightarrow\overline{abcdeg}\) chia hết cho 23 và 29
Chứng minh rằng abcdeg chia hết cho 23 và 29 , biết deg.2 bằng abc
Ta có : abcdeg = abc .1000 + deg
= ( deg . 2 ) . 1000 + deg
= deg . ( 2. 1000) + deg
= deg . 2000 + deg
= deg . ( 2000 +1)
= deg . 2001
= deg . (23 .29)
Ta thấy abcdeg là tích của deg và 23 và 29
=> abcdeg chia hết cho 23 và 29
Vậy abcdeg chia hết cho 23 và 29
tim abcdeg chia hết cho 23 và 29 biết rằng abc bằng 2 nhân deg
Ta có \(\overline{abcdeg}=1000\overline{abc}+\overline{deg}=2000\overline{deg}+\overline{deg}=2001\overline{deg}\)
Vì 2001 chia hết cho 23 và 29 =>\(2001\overline{deg}\)chia hết cho 23 và 29\(\Rightarrow\overline{abcdeg}\)chia hết cho 29 và 29
abcdeg = abc1000 +deg=deg x 2 x 1000 +deg =deg x 2000+ deg = deg x (2000+1)
= deg x 2001
Mà 2001 chia hết cho 23 và chia hết cho 29 nên 2001 x deg chia hết cho 23 và 29
Thiếu nữa nên mik viết tiếp: hay acbdeg chia hết cho 23 và 29
Chứng minh rằng abcdeg chia hết cho 23 và 29. Biết rằng abc= 2x deg
Ta có : abcdeg
= abc .1000 +deg
Lại có : abc = 2 deg
=>abcdeg = 2 deg .1000 +deg
= 2000 . deg + deg
= 2001 . deg
Hay abcdeg \(⋮\)23 và 29 (đpcm) vì 2001 =23.29.3
= 2001 . deg \(⋮\)23 và 29
các số abcdeg;abc;deg đều có gạch đầu nhé bạn
Dấu "." là dấu nhân nha bạn
1, Chứng minh abcabc chia hết cho 7 ; 11 và 13
2,Cho abc= 3 nhân deg . Chứng tỏ abcdeg chia hết cho 23
1) ta co abcabc=abc.1000+abc
= abc.1001 chia hết cho
vi 1001 chia het cho 7;11;13
=> abc.1001 chia het cho 7;11;13
=> abcabc chia het cho 7;11;13
2) trong câu hỏi tương tự nhé