Chứng minh các hệ thức sau: cos a - cos b 2 - sin a - sin b 2 = - 4 sin 2 a - b 2 cos a + b
PB
Những câu hỏi liên quan
Chứng minh các hệ thức sau:
\(\cot^2\alpha-\cos^2\alpha=\cot^2\alpha.\cos^2\alpha\)
Ta có \(VT=\cot^2a-\cos^2a=\frac{\cos^2a}{\sin^2a}-\cos^2a=\frac{\cos^2a-\cos^2a.\sin^2a}{\sin^2a}\)
\(=\frac{\cos^2a\left(1-\sin^2a\right)}{\sin^2a}=\frac{\cos^2a.\cos^2a}{\sin^2a}=\cot^2a.\cos^2a=VP\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Chứng minh các hệ thức sau:
a) \(\sin {20^o} = \sin {160^o}\)
b) \(\cos {50^o} = - \cos {130^o}\)
a)
\(\sin {20^o} = \sin \left( {{{180}^o} - {{160}^o}} \right) = \sin {160^o}\)
b)
\(\cos {50^o} = \cos \;({180^o} - {130^o}) = - \cos {130^o}\)
Đúng 0
Bình luận (0)
chứng minh các hệ thức sau không phụ thuộc vào \(\alpha\): \(\cos^4\alpha+\sin^2\alpha x\cos^2\alpha+\sin^2\)
Có: \(\sin^2+\cos^2=1\)
=> \(\sin^2=1-\cos^2\)
Ta có:
\(\cos^4a+\sin^2a\cos^2a+\sin^2a=\cos^4a+\left(1-\cos^2\right)a\cos^2a+\sin^2\)
\(=\cos^4a-\cos^4a+\cos^2a+\sin^2a=\cos^2a+\sin^2a=1\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn , các đường cao AM , BE , CF cắt nhau tại H . Chứng minh ta có hệ thức cos^2 A + cos ^2 B + cos^2 B = 1 - S của tam giác MEF
Cho A,B,C là các góc của tam giác. Chứng minh các đẳng thức sau: a. cos(A+B)+cosC=0 b. cosA+B/2=sinC/2 c. cos(A-B)+cos(2B+C)=0
a) \(cos\left(A+B\right)+cosC=0\)
\(\Leftrightarrow cos\left(\pi-C\right)+cosC=0\)
\(\Leftrightarrow-cosC+cosC=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
b) \(cos\left(\dfrac{A+B}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi-C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow sin\dfrac{C}{2}=sin\dfrac{C}{2}\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
c) \(cos\left(A-B\right)+cos\left(2B+C\right)=0\left(1\right)\)
Ta có : \(A+B+C=\pi\)
\(\Leftrightarrow2B+C=\pi-A+B\)
\(\Leftrightarrow2B+C=\pi-\left(A-B\right)\)
\(\left(1\right)\Leftrightarrow cos\left(A-B\right)+cos\left[\pi-\left(A-B\right)\right]=0\)
\(\Leftrightarrow cos\left(A-B\right)-cos\left(A-B\right)=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau
a) \(\dfrac{1-cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1+cos\alpha}\)
b)\(\dfrac{cos\alpha}{1+sin\alpha}+tg\alpha=\dfrac{1}{cos\alpha}\)
a) Cần chứng minh \(\dfrac{1-cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1+cos\alpha}\)
\(\Rightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha+cos^2\alpha=1\)
Giả sử tam giác ABC vuông tại A
Ta có: \(\left\{{}\begin{matrix}sin^2B=\dfrac{AC^2}{BC^2}\\cos^2B=\dfrac{AB^2}{BC^2}\end{matrix}\right.\Rightarrow sin^2B+cos^2B=\dfrac{AC^2+AB^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
Đúng 2
Bình luận (0)
a)\(\dfrac{1-cosa}{sina}=\dfrac{sina}{1+cosa}\)
<=>\(\left(1-cosa\right)\left(1+cosa\right)=sin^2a\)
<=>\(1-cos^2a=sin^2a\) (lđ)
b)Ta có VT=\(\dfrac{cosa}{1+sina}+tga=\dfrac{cosa}{1+sina}+\dfrac{sina}{cosa}=\dfrac{cos^2a+sin^2a+sina}{\left(1+sina\right)cosa}=\dfrac{1+sina}{\left(1+sina\right)cosa}=\dfrac{1}{cosa}=vp\left(dpcm\right)\)
Đúng 0
Bình luận (0)
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
(
A
)
sin
α
b
c
(
B
)
cotg
α
b
c
(...
Đọc tiếp
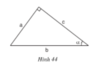
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
( A ) sin α = b c ( B ) cotg α = b c ( C ) tg α = a c ( D ) cotg α = a c
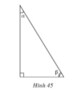
b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin ( 90 ° – α )
(D) tg α = sin α cos α
a) Chọn C
b) Chọn C sai
- Vì đẳng thức đúng phải là: cos β = sin ( 90 ° - β )
Đúng 0
Bình luận (0)
Chứng minh các hệ thức sau:
a) \(\frac{1-cos\alpha}{sin\alpha}=\frac{sin\alpha}{1+cos\alpha}\)
b) \(tan^2\alpha-sin^2\alpha=tan^2\alpha.sin^2\alpha\)
c) \(\frac{1-tan\alpha}{1+tan\alpha}=\frac{cos\alpha-sin\alpha}{cos\alpha+sin\alpha}\)
a) \(\frac{1-\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos a}\)
\(\Leftrightarrow\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=\sin^2\alpha\)
\(\Leftrightarrow1-\cos^2\alpha=\sin^2\alpha\)
\(\Leftrightarrow\sin^2\alpha+\cos^2\alpha=1\)( luôn đúng )
\(\Rightarrow\frac{1-\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos\alpha}\)
Chứng minh hệ thức sau:
\(\frac{\cos\alpha}{1-\sin\alpha}\)= \(\frac{1+\sin\alpha}{\cos\alpha}\)
\(\frac{cos\alpha}{1-\sin\alpha}=\frac{1+sin\alpha}{cos\alpha}\)
\(\Leftrightarrow cos^2\alpha=\left(1-sin\alpha\right)\left(1+\sin\alpha\right)\)
\(\Leftrightarrow cos^2\alpha=1-sin^2\alpha\)
\(\Leftrightarrow cos^2\alpha+sin^2\alpha=1\left(Đúng\right)\)
Đúng 0
Bình luận (0)




