Tính các giá trị lượng giác của góc α nếu
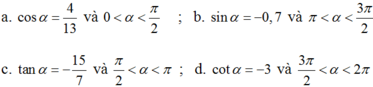
Tính các giá trị lượng giác còn lại của góc α biết sin α = 3 5
A. cos α = 3 4 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
C. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 3 4 ; tan α = 4 5 ; c o t α = 4 3
Ta có sin α = 3 5 suy ra sin 2 α = 9 25 , mà sin 2 α + cos 2 α = 1 , do đó:
cos 2 α = 1 - sin 2 α = 1 - 9 25 = 16 25 suy ra cos α = 4 5
Do đó:
tan α = sin α cos α = 3 5 : 4 5 = 3 5 . 5 4 = 3 4
c o t α = cos α sin α = 4 5 : 3 5 = 4 5 . 5 3 = 4 3
Vậy cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
Đáp án cần chọn là: B
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Với π/2 < α < π thì sinα > 0, cosα < 0, tanα < 0
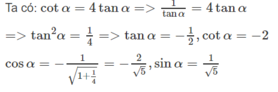
Tính các giá trị lượng giác của góc α, biết
cosα = 2sinα khi 0 < α < π/2
Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
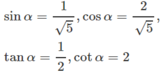
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
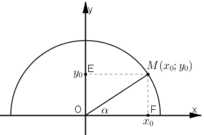
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 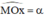
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0
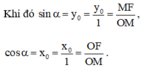
Cho cosα=\(\dfrac{1}{3}\) với 0<α<\(\dfrac{\pi}{2}\).Tính các giá trị lượng giác còn lại của góc α.
Em 2k8 ms học nên k chắc
Vì 0 < \(\alpha< \dfrac{\pi}{2}\) => sin \(\alpha>0\)
Cos \(\alpha=\dfrac{1}{3}\) \(\Rightarrow sin\alpha=\sqrt{1-\dfrac{1}{9}}=\dfrac{2\sqrt{2}}{3}\)
tan \(\alpha=2\sqrt{2}\) ; cot \(\alpha=\dfrac{1}{2\sqrt{2}}\)
Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.
\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)
Tính các giá trị lượng giác của cung α biết
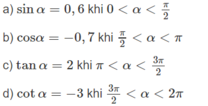
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)