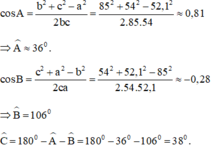So sánh các cạnh của tam giác ABC, biết rằng: Â = 80º, B̂ = 45º
PB
Những câu hỏi liên quan
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
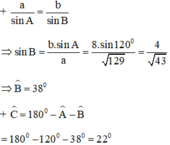
Đúng 0
Bình luận (0)
Tính các góc của tam giác ABC . Biết rằng Â= 2B̂ = 3C
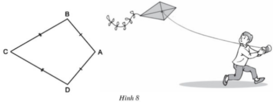
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD.
b) Tính B̂,D̂ biết rằng  = 100º, Ĉ = 60º
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
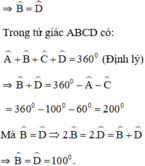
Đúng 0
Bình luận (0)
So sánh các cạnh của tam giác ABC biết rằng ∠A = 80o, ∠C = 40o
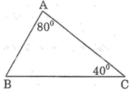
Ta có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠B = 180o - (∠A + ∠C )
= 180o - (80o + 40o) = 60o
Trong ΔABC, ta có: ∠A > ∠B > ∠C
Suy ra: BC > AC > AB (đối diện với góc lớn hơn là cạnh lớn hơn).
Đúng 0
Bình luận (0)
Cho ΔABC có AB < BC < CA, thế thì:
A. Â> B̂
B. B̂< 60o
C. B̂= 60o
So sánh các cạnh của tam giác ABC, biết rằng: góc A = 80 độ ,góc B = 45 độ
goc A > goc C > goc B dung bam dung cho nhe
Đúng 0
Bình luận (0)
Xét tam giác ABC có A+B+C=180 độ =>C=180-80-45=55 độ
Ta lại có A>C>B=>BC>AB>AC
Đúng 0
Bình luận (0)
1) Không cần vẽ hình hãy so sánh các góc của tam giác ABC, biết rằng:
AB=5cm, AC= 6cm, BC=7cm
2) Không cần vẽ hình hãy so sánh các cạnh của tam giác ABC, biết rằng: góc A = 65 độ, góc B = 70 độ
3) Hãy kiểm tra xem bộ ba đoạn thẳng 18cm, 6cm, 11cm có là ba cạnh của một tam giác hay không? Vì sao?
1/ Ta có BC > AC > AB (7cm > 6cm > 5cm) => \(\widehat{A}>\widehat{B}>\widehat{C}\) (quan hệ giữa góc và cạnh đối diện trong tam giác)
2/ Ta có \(\widehat{C}=180^o-\widehat{A}-\widehat{B}\)(tổng ba góc của một tam giác)
=> \(\widehat{C}\)= 180o - 65o - 70o = 45o
=> \(\widehat{B}>\widehat{A}>\widehat{C}\)=> AC > BC > AB (quan hệ giữa góc và cạnh đối diện trong tam giác)
3/ Ta có 18cm > 6cm + 11cm = 17cm không thoả mãn bất đẳng thức tam giác
=> Bộ ba (18cm; 6cm; 11cm) không phải là ba cạnh của một tam giác
Đúng 0
Bình luận (0)
Cho tam giác ABC có Â = 120o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).
Đúng 0
Bình luận (0)